Solution – Nombres Complexes – Applications Géométriques

Solution – Nombres Complexes – Applications Géométriques – s2477
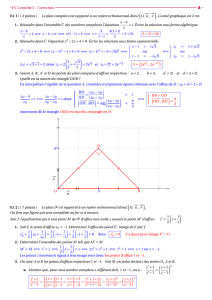
1/ Montrer que, pour tout z , z' ∈∈ IC : | z + z' |2 + | z – z' |2 = 2(| z |2 + | z' |2) .
Soit z = x + iy et z' = x' + iy' .
z + z' = (x + x') + i(y + y') ⇒ | z + z' |2 = (x + x')2 + (y + y')2 .
z – z' = (x – x') + i(y – y') ⇒ | z – z' |2 = (x – x')2 + (y – y')2 .
| z + z' |2 + | z – z' |2 = (x2 + 2xx' + x'2 + y2 + 2yy' + y'2) + (x2 – 2xx' + x'2 + y2 – 2yy' + y'2)
| z + z' |2 + | z – z' |2 = 2[(x2 + y2) + (x'2 + y'2)] = 2(| z |2 + | z' |2) .
2/ Soient M , N , P les points d'affixes respectives z , z' , z + z' .
Interpréter géométriquement le résultat du 1/ .
z est l'affixe de → OM ,
z' est l'affixe de → ON ,
z + z' est l'affixe de → OM + → ON = 2 → OI = → OP .
Ceci prouve que le quadrilatère (OMPN) est un parallélogramme.
z – z' est l'affixe de → OM – → ON = → NM .
| z + z' |2 + | z – z' |2 = 2(| z |2 + | z' |2) ⇔ OP2 + MN2 = 2(OM2 + ON2) .
Dans un parallélogramme, la somme des carrés des longueurs des diagonales est égale à la somme des carrés des
quatre côtés du parallélogramme.