LABORATOIRE 4 FORCE CENTRIPÈTE

1
L ABORATOIRE 4 F ORCE CENTRIPÈTE
BUT
• Acquérir une meilleure compréhension de la cinématique
et de la dynamique du mouvement circulaire uniforme
(MCU)
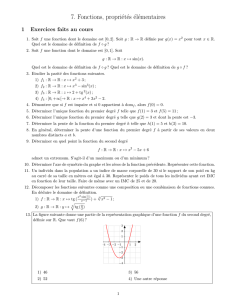
• Valider l’application de la deuxième loi de Newton au
mouvement circulaire uniforme en mesurant la masse
d’inertie m d’un mobile en rotation (voir illustration).
MATÉRIEL REQUIS
• Montage pour l’étude du mouvement de rotation;
• Chronomètre;
• Ensemble de masses marquées (précises à 1 % près);
• Balance.
MISE EN SITUATION
Lorsque la masse m est en rotation, la seule force agissant
sur elle horizontalement est la force du ressort. Cette force
étant dirigée vers le centre de rotation, il s’agit d’une force
centripète. Cette force est donc directement liée à
l’accélération centripète subie par la masse.
MANIPULATIONS
• Détachez la masse m du système et mesurez sa masse sur
la balance. Ce sera la valeur théorique m.
m
th
= (_______ ± _______) g.
• Raccrochez la masse uniquement à ses cordes de support
pour commencer, et assurez-vous que la tige horizontale
soit centrée sur l’axe vertical, pour éviter tout
débalancement. Assurez-vous ensuite que le repère
vertical fixé à la base soit parfaitement vis-à-vis la pointe
de la masse mobile m. Rattachez ensuite le ressort à la
masse.
• Le montage étant au repos, suspendez une masse M de
600 g à la corde fixée à la masse mobile (via la poulie), et
tirez et fixez la chainette de façon à ramener la masse m
vis-à-vis le repère. Vous pourrez donc déterminer la force
de rappel du ressort lorsqu’il est ainsi étiré.
• La position de la tige horizontale et du repère fixe ne
devraient plus bouger pour le reste de vos manipulations.
Notez ensuite la distance r entre le repère fixe et l’axe
vertical (attention, l’axe de rotation est le centre de la tige
verticale). Soyez minutieux et évaluez une incertitude
adéquate.
r = (______ ± ______) cm
• Détachez la masse suspendue et mettez le système en
rotation à vitesse constante, de telle sorte que la masse
mobile passe vis-à-vis le repère fixe à chaque passage.
• À l’aide d’un chronomètre, mesurez la durée de 20 rotations
et inscrivez votre résultat dans le tableau fourni. Évaluez
également une incertitude raisonnable sur cette durée totale
de 20 tours. Inscrivez la valeur trouvée dans le tableau. La
corde verticale est-elle bien verticale durant la rotation?
• Refaites les manipulations précédentes avec des masses M
de 525 g, 450 g, 375 g et 300 g. Vous devriez pouvoir
ajuster la position de la masse mobile uniquement en
modifiant la fixation du ressort sur l’axe (chainette). Ainsi,
le rayon sera le même pour toutes les configurations et
l’analyse assumera la constance de cette valeur.
ANALYSE
Complétez le tableau fourni en calculant l’inverse de la masse
M et le carré de la période de rotation.
Faites un graphique de « T
2
» en fonction de « 1/M », dans le
but que la pente contienne la valeur de la masse mobile m.
À partir des équations du système rédigées à l’aide des
diagrammes de forces, établissez une équation liant T² et le
rapport (1/M) (c'est-à-dire une équation de type T² = f(1/M)).
Cette équation contiendra la variable m et quelques autres
paramètres connus.
Déterminez si la relation mise en graphique devrait passer par
l’origine (en déterminant quelle serait le carré de la période si
l’inverse de la masse M tendait vers 0). Si c’est le cas, vous
pouvez forcer le passage de la droite par (0, 0).
Établissez le lien entre la pente du graphique (désignons la
pente par la variable a) et la valeur de la masse en rotation m,
et calculez sa valeur. Ce sera la valeur expérimentale, m
exp
.

2
RAPPORT
• Schémas/diagrammes de forces de la situation réalisée (au
repos (2 masses) ET en rotation). Peuvent être faits à la
main après impression, sur un espace réservé.
• Établissez le système d'équations décrivant le système (au
repos ET en rotation).
• Tableau reproduit et complété ( incertitudes incluses).
(Attention, les incertitudes peuvent différer dans une
même colonne. Si c’est le cas, vous devez modifier le
tableau pour que chaque valeur ait son incertitude, ou
appliquer la plus grande incertitude à toutes les valeurs.)
• Graphique T² = f (1/M)
• Démonstration du lien entre T², (1/M) et m à partir des
équations du système, et expression algébrique de m en
fonction de la pente.
• Calculs de m à partir de la pente du graphique.
Calcul de l’incertitude sur m à partir de l’incertitude
sur la pente du graphique, qui vous permettra de calculer
m
exp
via la « valeur centrale ». (Le graphique doit montrer
les pentes minimale et maximale, mais les étapes
préalables et les calculs n’ont pas à être fournis.)
• Pourcentage d’écart entre m
exp
et m
th
, et comparaison
graphique.
• Date de remise : _______________________
TABLEAU
Essai Charge à l’équilibre Durée de 20 tours Inverse de la masse M Carré de la période
M t
20
1/M T
2
(g) (s) (g
-1
) (s
2
)
±
1 600 ± ± ±
2 525 ± ± ±
3 450 ± ± ±
4 375 ± ± ±
5 300 ± ± ±
m
th
= (_______ ± _______) g
r = (______ ± ______) cm
Compléments d’information
Les notions d’incertitude sur la pente d’une droite et de comparaison graphique de valeurs avec incertitude sont décrites
dans des fichiers distincts disponibles sur le site Internet du cours.