Sinus et Cosinus

Chap 09_Livre_3eme_sinus_cosinus 21/04/2008
2
3
87,0
1
87,0
60sin
2
2
707,0
1
707,0
45sin
2
1
5,0
15,0
30sin
2
1
5,0
15,0
60cos
2
2
707,0
1
707,0
45cos
2
3
87,0
1
87,0
30cos
hypoténuse
opposécôté
hypoténuse
opposécôté
hypoténuse
opposécôté
hypoténuse
adjacentcôté
hypoténuse
adjacentcôté
hypoténuse
adjacentcôté
6,729'5
000174533,0 999999985,0
99,89tan
73,1
5,087,0
60tan
1
707,0 707,0
45tan
58,0
87,0 5,0
30tan
0
1
0
0tan
adj
opp
adj
opp
adj
opp
adj
opp
adj
opp
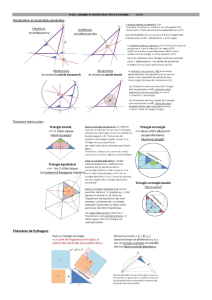
= 30°
= 60°
R = 1
R = 1
adj = 0,87 adj = 0,5
opp = 0,5
opp = 0,87
R = 1
opp = 0,707
= 45°
adj = 0,707
Sinus et Cosinus

Chap 09_Livre_3eme_sinus_cosinus 21/04/2008
Démonstration avec l’aide du théorème de Pythagore
Valeur de sin 45° et de cos 45°
2222 2ABACABBC  car AB = AC
Si BC = 1, alors :
707,0
2
2
22
21
2
1
2
1
2
1
21
2
22
AB
AB
AB
Valeur de sin 30° et de cos 60°
Tracer D, symétrique de B par rapport à A.
Par symétrie, le triangle BCD est donc équilatéral et
1 BCBD
donc : 5,0
2 BD
AB
Dans un triangle rectangle dont l’hypoténuse BC vaut 1 :
- AB, côté adjacent à l’angle de 60°, représente le cosinus ;
- AB, côté opposé à l’angle de 30°, représente le sinus.
Ainsi :
2
1
5,0
15,0
60cos
2
1
5,0
15,0
30sin
hyp
adj
hyp
opp
Valeur de sin 60° et de cos 30°
Selon Pythagore :
866,0
2
3
4
3
4
3
4
1
1
2
1
12
222
222
AC
ABBCAC
ACABBC
Dans un triangle rectangle dont l’hypoténuse BC vaut 1 :
- AC, côté adjacent à l’angle de 30°, représente le cosinus ;
- AC, côté opposé à l’angle de 60°, représente le sinus.
Ainsi, 866,0
2
3
60sin30cos 
A
B
C
45°
45°
1
A
B
C
30°
60°
1
D
A
B
C
30°
60°
1
D
1
2