vitesses d`ondes

vitesses d’ondes
A l’aide des documents vidéo, répondre à l’interrogation suivante :
Peut-on estimer que l’onde se propage à vitesse constante ?
Méthode :
•Rédiger un protocole permettant de répondre à l’objectif
•Par l’usage des logiciels déterminer les grandeurs nécessaires
•Rédiger clairement l’ensemble de votre résolution : tableau de mesures, graphes etc..
•La relation théorique donnée pour la vitesse est-elle compatible avec les mesures.
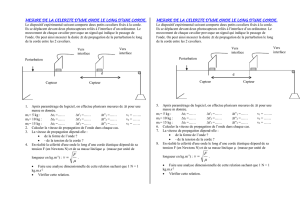
Corde tendue Corde non tendu
1- ONDES le long d’une corde

1ere étape : protocole
A l’aide des séquences vidéo et du logiciel de pointage , on peut relever la position du front
de l’onde sur la corde (x) au cours du temps (t).
Il suffit de tracer x = f(t) dans Excel et de vérifier si x est proportionnel à t . Alors x=f(t) sera
linéaire et le coefficient directeur de droite représentera la valeur constante de la vitesse.
X=f(t) du type x (m)= v(m/s).t (s) linéaire avec v = cte en m/s
2- Par l’usage des logiciels déterminer les grandeurs nécessaires
On obtient 2 graphes x=f(t) pour les 2 cas
Corde tendue Corde non tendue

3ème étape : Rédiger clairement l’ensemble de votre résolution : tableau de mesures, graphes
etc..
Corde tendue Corde non tendue
X = 10.7 x t
X= v x t Donc v = 10.7 m/s
EXCEL : y=10.724t
EXCEL : y=16.683t
X = 16.7 x t
X= v x t
Donc v = 16.7 m/s
X=f(t) linéaire dans les deux cas donc la vitesse reste constante lors de la propagation
La relation théorique donnée pour la vitesse est-elle compatible avec les mesures.
mesures : Plus la corde est tendue plus la vitesse est grande
Théorie : v=
donc si la tension F de la
corde F augmente la
vitesse augmente
F
µ
Tension de la corde (N)
Masse linéique (kg/m)
Conclusion : cela correspond aux résultats expérimentaux

2- croisement d’ondes
La vitesse d’une onde est-elle modifiée quand elle en croise une autre ?
1- protocole : Il suffit de suivre la position du front d’une vague au cours du
temps à l’aide du logiciel de pointage. Si la vitesse ne change
pas après le croisement des vagues, le
graphe x= f(t) sera une droite
2- Résultats des mesures
Avant le
croisement
Après le
croisement
x=f(t) est une droite et garde le
même coefficient directeur donc
la vitesse reste constante ( égale
à 21.4 cm/s)
3- interprétation
Conclusion:
La vitesse d’une onde n’est
pas modifiée quand elle en
croise une autre
Y=0.214x
La profondeur de la nappe d’eau est-elle constante?
La vitesse d’une onde dépend la profondeur de l’eau, ici la vitesse est
constante dans toutes les directions, car les fronts d’onde sont
parfaitement circulaires.
On pourrait le vérifier en faisant des pointages dans des directions
différentes.