I. Le cercle trigonométrique, abscisse curviligne. O

Classe de
1S1
Trigonométrie.
I. Le cercle trigonométrique, abscisse curviligne.
O,I,J
est un repère orthonormal.
1. Le cercle trigonométrique .
Définition le cercle trigonométrique est le cercle C de centre O de
rayon 1, orienté d'un sens appelé direct et choisi arbitrairement (en
général on choisit le sens contraire des aiguilles d'une montre).
2. Enroulement de la droite réelle sur le cercle trigonométrique.
Lorsque le zéro de la droite des réels coïncide avec le point I sur le cercle on enroule la demi-droite
des réels positifs sur le cercle dans le sens positif choisi et la demi-droite des réels négatifs dans le
sens contraire.
Chaque point M du cercle est ainsi recouvert par une infinité
de nombres réels tous appelés abscisses curvilignes du point
M.
Proposition. Si
et
'
sont deux abscisses curvilignes de M
alors elles diffèrent d'un multiple entier de
2
.
Autrement dit il existe un entier k tel que
− '=k×2
.
Conséquence : Si
est une abscisse curviligne de M toutes
les autres s'écrivent
k×2
✍ Voir exercices corrigés 12 à 17 page 299.
Proposition. Parmi toute les abscisses curvilignes d'un point une seule appartient à l'intervalle
[
− ;
]
: c'est l'abscisse curviligne principale.
S. Baudet page 1 sur 3. classe de 1ère S1.
+
Quelques repérages sur le cercle
trigonométrique

Classe de
1S1
Trigonométrie.
II Le radian.
Définition. Le radian est la mesure d'un angle au centre qui intercepte sur le cercle de rayon 1 un
arc de longueur 1
Définition (bis) Le radian est la mesure d'un angle
au centre qui intercepte sur le cercle un arc de
longueur égale à son rayon r. (voir exercice 22 page
300)
La mesure en radian d'un angle correspond à la longueur de l'arc intercepté par cet angle au centre
sur le cercle trigonométrique.
Proposition. Les mesures en radians et en degrés d'un angle sont proportionnelles
radian
2
3
4
6
degré 180° 90° 60° 45° 30°
✍Voir exercices 19 et 20 page 300
S. Baudet page 2 sur 3. classe de 1ère S1.
1

Classe de
1S1
Trigonométrie.
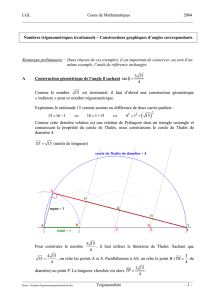
III. Angle orienté et mesure.
Tout couple de vecteurs
u,
v
défini un angle
orienté unique. (mais pas de mesure unique !)
Si t est une abscisse curviligne de A et si
t '
est une
abscisse curviligne de B alors une mesure de l'angle
u,
v
est :
t ' −t
(observez bien l'ordre)
et
sont les longueurs des deux arcs
AB
.
Alors deux mesures en radian de l'angle orienté
u,
v
sont
et
−
.
L'une des deux appartient à
]
− ,
]
(sur ce schéma
−
), c'est la mesure principale de
l'angle
u,
v
(elle correspond au plus petit arc géométrique).
Si
est une mesure de l'angle
u,
v
toutes les autres sont les nombres :
k×2
où
k∈
ℤ
Exemple:
mes(
u,
v
)=..............
•mes(
u,
w
)=..............
•mes(
v,
w
)=..............
Exercices
Trouver les mesures principales de :
31
3
−23
6
16
5
−127
4
Angles particuliers.
Dorénavant on identifie l'angle et ses mesures... on écrit
u,
v
=
5
2
(lire égal à « pi
sur 5 modulo deux pi » ) ou
u;
v
=
5k×2
,
k∈ ℤ
•l'angle nul
u,
v
=
u,
v
=
O=0
2
•l'angle plat
u,−
u
=
=
2
•l'angle droit
i,
j
=
2
2
j,
i
=−
2
2
est appelé angle droit indirect .
(
O;⃗
i,⃗
j
)
et
(
O;⃗u,⃗v
)
sont des repères orthonormaux directs.
(
O;⃗
i,−⃗
j
)
est un repère orthonormal indirect.
S. Baudet page 3 sur 3. classe de 1ère S1.
β
α
1
/
3
100%