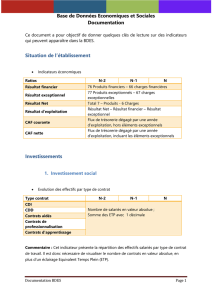
e somme des inverses des « k parmi n - E

131201-Suites-ehrs-SommDesInvDesCnp-ColPcsia-AML65monchEx2
sur un total de points de :
E SOMME DES INVERSES DES « K PARMI N »
e1 Soit un=la somme pour k allant de 0 à n des « 1/(le coefficient
binomial « k parmi n »). On s'intéresse à la limite des un. On pourra
considérer n>=6 et poser vk=1/(k parmi n) et wk=(k parmi n). On a
donc un=somme des vk. Montrer que un>=2
e2 Pour tout entier k pris dans [[ 2 ; n-2 ]], montrer que wk>=w2
e3 En déduire que un est encadrée par deux suites à convenir
E4 Quelle est la limite de la suite u ?
H SOMME DES INVERSES DES « K PARMI N »
h1 Dessiner les 3 premières lignes du triangle de Pascal de votre
Tale...
Et ça tombe tout seul !
h2
Remarquer qu'on peut se ramener à 2<=k<=E(n/2)<=n/2. Pourquoi ?
Etudier la suite finie des nombres : w_k = (k parmi n) pour k entre 2 et n/2
Poser 2<=k<=k+1<=n/2 A quoi ça peut servir ?
h3
H4
R SOMME DES INVERSES DES « K PARMI N »
r1
r2
Dessiner un début de triangle de pascal de nouveau. Il est clair que les Cnk semblent strictement
croissants pour k allant de 2 à n/2. Ce qui donnera Cnk>=Cn2. Par symétrie, on obtient cette
minoration aussi pour les k de n/2 à n-2
Attention le calcul direct Cnk / Cn2 est poussif avec beaucoup d'indices à gérer. Par contre de
proche en proche, ça va bien et ça tombe en ½ ligne.
[email protected] http://SitSit33.e-monsite.com © AML ; 03/12/13 ; p 1 / 3

Soit k tel que 2<=k<=k+1<=n/2.
w_(k+1) / w_k = n ! / n ! * k ! / (k+1) ! * (n-k) ! / (n-k-1) !
Ce n'est pas indigeste ! J'ai groupé les « ! » par division qui vont bien
et on ne perd pas le nord en se rappelant que chez nous k est petit
= (n-k)/(k+1) dont on cherche à montrer qu'il est >=1 (toujours SOOV*)
en gros, c'est parce que k ne dépasse pas la moitié que ça va marcher
= (n-k-1+1)/(k+1) OR n/(k+1)>=2 et (-k-1)/(k+1)=1, donc
= n/k+1 + (-k-1)/(k+1) + 1/(k+1) >= 2-1 cqfd, ce qui prouve que la suite (wk) pour k
de 2 à n/2 est croissante donc wk>=w2
r3
Donc : w0=wn=1 w1=w_(n-1)=n wk>=w2=n(n-1)/2 pour tous les autres k de 2 à n-2 qui
sont au nombre de n-3
On a donc montré que : 2<=un<=2 + (2/n) + (n-3) * 2/(n(n-1))
R4
Par le théorème des gendarmes, lim un = 2
S SOMME DES INVERSES DES « K PARMI N »
s1
S2
S3
[email protected] http://SitSit33.e-monsite.com © AML ; 03/12/13 ; p 2 / 3

Didactisons donc Un Peu Ensemble !
Formules :
2
x−x2
x1
Vous aurez ds ce fichier :
E : l'énoncé
H : les indications (ou Hints en anglais)
R : les réponses rédigées
S : les remarques de synthèse.
Bonne lecture !
[email protected] http://SitSit33.e-monsite.com © AML ; 03/12/13 ; p 3 / 3