trigonometrie

315DP6
TRIGONOMETRIE
Leçon 1
© www.maths974.fr
à
à
15 mm
35 mm
30 mm
I. COSINUS, SINUS, TANGENTE D’UN ANGLE AIGU
a. Vocabulaire et notation
Le cosinus, le sinus et la tangente d’un angle aigu sont des nombres.
On les note ainsi : cos , sin et tan .
 Exemple : avec la calculatrice en mode degrés taper sin (53) et donner une valeur arrondie à 0,01 près :
sin(53°)
………….
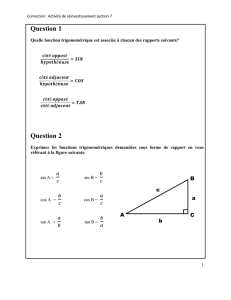
b. Définitions dans un triangle rectangle
Dans un triangle rectangle avec un angle aigu, on peut calculer les nombres cos , sin et tan
grâce aux formules suivantes :
cos =côté adjacent à
hypoténuse
sin =côté opposé à
hypoténuse
tan =côté opposé à
côté adjacent à
cosBAC
=AB
AC sin BAC
=BC
AC tan BAC
=BC
AB
 Exemple : Soit RTL un triangle rectangle en R. Compléter les formules en
couleur, remplacer par les nombres et calculer (valeur exacte et
valeur arrondie à 0,01 près)
 cos
RTL
=  cos
RLT
=
cosRTL =...........
........... (valeur exacte)
cosRTL
............ (valeur arrondie à 0,1 près)
cosRLT =...........
........... (valeur exacte)
cosRLT
............ (valeur arrondie à 0,1 près)
 sin
RTL
=  sin
RLT
=
sin RTL =...........
........... (valeur exacte)
sin RTL
............ (valeur arrondie à 0,1 près)
sin RLT =...........
........... (valeur exacte)
sin RLT
............ (valeur arrondie à 0,1 près)
 tan
RTL
=  tan
RLT
=
tanRTL =...........
........... (valeur exacte)
tanRTL
............ (valeur arrondie à 0,1 près)
tanRLT =...........
........... (valeur exacte)
tanRLT
............ (valeur arrondie à 0,1 près)
 Remarque : le cosinus et le sinus d’un angle aigu sont des nombres compris entre 0 et 1.

315DP6
TRIGONOMETRIE
Leçon 2
© www.maths974.fr
 Astuce pour se souvenir des formules :
II. APPLICATIONS DANS UN TRIANGLE RECTANGLE
a. Calculer un côté d’un triangle rectangle (utilisation du produit en croix)
Soit RTL un triangle rectangle en R tel que RL = 6 cm et
RLT
= 43°.
Calculer RT.
Ecrire les trois formules de trigonométrie avec l’angle ………
Remplacer par les nombres. Entourer la formule qui va convenir pour
calculer RT.
Solution :
Dans le triangle RTL,
on a
soit
d’où RT = (valeur exacte de RT)
donc
RT 
à 1 mm près.
b. Calculer un angle aigu dans un triangle rectangle. (utilisation de cos -1 ou sin -1 ou tan -1 )
Soit XYZ un triangle rectangle en X tel que XY = 4 cm et YZ = 6 cm. Calculer
XZY
(arrondir au degré).
Ecrire les trois formules de trigonométrie avec l’angle ………
Remplacer par les nombres. Entourer la formule qui va
convenir pour calculer
XZY
.
Solution :
Dans le triangle XYZ,
on a
soit
d’où
XZY
(en utilisant la touche……….. )
CAH SOH TOA*
* Casse-toi !
4 cm 6 cm
XZ
Y
43° 6 cm
L
R
T