Chapitre 4 A. FONCTIONS USUELLES CLASSIQUES I. FONCTION

23
Chapitre 4
A. FONCTIONS USUELLES CLASSIQUES
I. FONCTION LOGARITHME
1° Fonction logarithme népérien
a) Théorème 1 et définition 1
La fonction logarithme népérien, notée ln, est l'unique primitive sur
*
de
1
x
x
, qui s'annule en 1.
Elle est donc définie par :  x > 0, ln(x) =
1
xdt
t
et on a : ln(1) = 0
Propriété fondamentale : (x,y)  (
*
)2 , ln(xy) = ln(x) + ln(y)
b) Formulaire :
(1)  t > 0 ,
tt
1
ln( ) ln( )
, (x,y)  (
*
)2 , ln(
x
y
) = ln(x)  ln(y) ; ln(e) = 1
(2)  x 
*
,  n  ,
ln( ) ln( )
n
x n x
(3)
lim ln( )
xx
,
0
lim ln( )
xx
(4) Si u est dérivable sur un intervalle I, avec :  x  I,
ux( ) 0
.  x  I,
ux
ux ux
()
[ln( ( ) )] ()
2° Fonction logarithme décimal
a) Définition 2
On appelle logarithme décimal (ou de base 10) , l'application, notée
log
, ou
10
log
, définie sur
*
par :  x > 0,
ln( )
log( ) ln(10)
x
x
(Remarque :
ln(10) 2, 3
)
b) Propriétés fondamentales :
log
(1) = 0 ,
log(10)
= 1,
 (x,y)  (
*
)2,
log( ) log( ) log( )xy x y
 x   ,
log(10 )
xx
, x  +,
log( )
10 xx
c) Application Le logarithme décimal est utilisé en chimie (pH = 
log([ ])H
.
II. FONCTIONS EXPONENTIELLES
1° Fonctions exponentielle de base e
a) Définition 3
D'après les propriétés du logarithme : Pour tout x  , l'équation [ln(t) = x ], d'inconnue t, admet une unique
solution strictement positive. Elle est notée provisoirement exp(x). Cela permet de définir une fonction de 
dans
*
, appelée fonction exponentielle, qui est la fonction réciproque du logarithme népérien :
 x > 0,  y   , y = ln(x)  x = exp(y)
Elle est dérivable sur , égale à sa dérivée et on a la propriété fondamentale :
 (x,y)  ² ,
exp( ) exp( ). exp( )x y x y
FONCTIONS USUELLES DE VARIABLE RÉELLE

24
Par définition, e = exp(1), il s'ensuit immédiatement, par récurrence sur n :  n  , exp(n) =
n
e
Pour généraliser cette écriture, on note, pour tout x réel : exp(x) =
x
e
La propriété fondamentale s’écrit alors, de façon définitive :  (x,y)  ²,
x y x y
e e e
b) Formulaire avec notation définitive
(1)  x  , ln(
x
e
) = x et  a > 0,
ln( )a
e
= a
(2)  t   ,
t
t
e
e1
,  (x,y)  ²,
x
y
xy e
e
e
(3)  x  ,  n   ,
()
x n nx
ee
(4)
lim ( )
x
xe
,
lim ( ) 0
x
xe
(5) Si u est dérivable sur I, alors
()ux
xe
est dérivable sur I et on a :  x  I,
u x u x
e u x e
( ) ( )
( ) ( )
2° Fonctions exponentielle de base a avec a 
*
(« bord programme »)
a) Définition 4
On définit la fonction exponentielle de base a, notée provisoirement
expa
, par :  x  ,
ln( )
exp ( ) xa
axe
.
* Elle vérifie la propriété fondamentale :  (x,y)  ²,
exp ( ) exp ( ). exp ( )
a a a
x y x y
* On a immédiatement :
exp (1)
aa
et par récurrence sur n :  n  ,
exp ( )
an
=
n
a
* Toujours par extension, on note alors, pour tout x réel :
x x a
ae
ln( )
b) Remarques :
R1 Lorsque n est entier,
ln( )na
n
ae
est égal à
facteurs
......
n
a a a
.
R2 Relation avec le logarithme (
1a
) :
xa
x
y a e ln( ) ()
ln( )
ln( )
ln( ) ln( ) ln( ) y
a
x
y a x a x
c) Formulaire avec notation définitive
(1)
01a
;  (x,y)  ² ,
x y x y
a a a
(2)
x
ya
ln( ) ln( ) ln( )
x
y a x a
(3)  t  ,
11
()
t
tt
a
a
a
;  (x,y)  ²,
x
xy
y
a
aa
(4)  x  ,  y   ,
()
x y xy
aa
(5) si a > 1 ,
lim ( )
x
xa
,
lim ( ) 0
x
xa
(formules échangées pour a  ]0,1[ )
(6)
x
xa
est dérivable sur  et :  x   ,
( ) ln( ).
xx
a a a
d) Définition de fonctions à exposant variable
Lorsqu’une fonction u définie sur I est strictement positive sur I et la fonction v est définie de I dans ,
on peut définir une fonction f, pour tout x  I :
( ) ( )ln( ( ))
( ) [ ( )]
v x v x u x
f x u x e
Si u et v sont alors continues sur I (respectivement dérivables sur I), alors
v
fu
est continue sur I
(respectivement dérivable sur I).
III. GÉNÉRALISATION DES FONCTIONS PUISSANCES
1° Propriétés algébriques
a) Définition 5
Soit a  . On appelle fonction puissance a, la fonction
a
définie sur
*
par :
ln( )
() ax
axe
b) Remarque élémentaire

25
Pour n  , la fonction
n
coïncide sur
*
avec la fonction habituelle
n
xx
.
On étend alors la notation en posant :
ln( )
() a x a
ax e x
c) Formules algébriques :  (x,y) 
*2
,  (a,b) 
2
,
()
a a a
x y xy
;
a b a b
x x x
,
()
a b ab
xx
2° Étude fonctionnelle sur
*
(a  *)
a) Limites : Si a < 0, alors :
0
lim ( )
a
xx
et
lim ( ) 0
a
xx
.
Si a > 0, alors :
0
lim ( ) 0
a
xx
et
lim ( )
a
xx
.
Dans ce dernier cas, la fonction
a
est prolongée en 0 par :
(0) 0
a
b) Tangente au point O dans le cas a > 0 :
Si a  ]0,1[, alors la courbe a admet en O une tangente verticale.
Si a  ]1,+[, alors la courbe a admet en O une tangente horizontale.
c) Proposition 1 Variations et tracés sommaires
*
a
est dérivable sur
*
et :  x > 0,
1
() a
ax ax
(se fait en écrivant
ln( )
() ax
axe
)
** a > 0
a  ]0,1[ : a  ]1,+[ :
*** a < 0
3° Propriétés de bijectivité
a) Proposition 2 Pour a
0
,
a
xx
est une bijection de
*
sur
*
et l’application réciproque est
1a
xx
Pour a  , la fonction
a
xx
est naturellement prolongée sur , et pour a  , elle est prolongée sur *.
Dans le cas a impair positif,
a
xx
est une bijection de  sur  ; dans le cas a impair négatif,
a
xx
est une
bijection de * sur *.
b) Cas particulier
Pour a = 2,
xx
2
est une bijection de sur et l’application réciproque est
1
2
x x x
.
c) Racine nème : (« bord programme »)
 Si n est pair,
n
xx
définit une bijection de sur . Sa fonction réciproque, notée
1n
xx
, est
appelée fonction racine nème, définie sur , notée aussi :
n
xx
.  x  0,
,( )
nn
nn
x x x x

26
 Si n est impair,
n
xx
définit une bijection de sur . Sa fonction réciproque, notée
1n
xx
, est
appelée fonction racine nème, définie sur , notée :
n
xx
.  x  ,
,( )
nn
nn
x x x x
Formules simples :  (x,y) 
2
,  (n,p) 
2
*
,
1 1 1
()
n n n
x y xy
;
11
1
()
p np
n
xx
Exemples :
382
,
1 1 1
4 4 4 4
4
32 (16 2) (2 2) 2 2
,  x > 0,
3
63
x x x
4° Croissances comparées
a) Théorème 2 Comparaison des fonctions puissances et logarithmes
(1)  a > 0 ,
ln( )
lim 0
a
x
x
x
(I)  a > 0 ,  b > 0,
b
a
x
x
x
ln ( )
lim 0
(2)  a > 0 ,
0
lim ln( ) 0
a
xxx
(II)  a > 0 ,  b > 0,
0
lim ln( ) 0
b
a
x
xx
 En terminale, on a vu que :
x
x
x
ln( )
lim 0
(T) ; en effet :  x  1, 0  ln(x) =
xx
t
dt dt
t
11
.
On calcule cette intégrale :
xx
t
dt tx
1
1[2 ] 2 2
. L’encadrement:
ln( ) 22
0x
xx
x
, valable pour x  1,
permet de conclure pour la limite (T).
(1) Pour a > 0 :
ln( ) 1 ln( )
a
aa
xx
x a x
. Or
lim ( )
a
xx
. Donc par composition des limites, on a le résultat.
(I) On transforme la fraction :
a
b
b
b
b
a
xx
X
xx
ln ( ) ln( )
et donc, d’après (1),
ln( )
lim 0
a
xb
x
x
, et comme
0
lim( ) 0
b
xX
, on conclut par composition des limites.
(2) et (II) On pose :  x < 1,
x
X1
et alors :
0xX
. Les égalités
ln( )
ln( ) a
aX
X
xx
et
ln ( )
ln( ) b
a
b
aX
X
xx
permettent de conclure facilement. 
b) Théorème 3 Comparaison des fonctions puissances et exponentielles
  > 0,
0
, (1)
xx
xx
exe
x
lim lim
(2)
x
xxelim 0
 (1) on pose :
x
te
;
xt
. L’égalité
x
et
xtln ( )
permet de conclure grâce au théorème 3
(2) Se déduit de (1) en posant
yx
, y > 0, d’où l’égalité :
x
y
xe ye
1
qui permet d’utiliser (1).
c) Autre écriture de (1) : Soit a un réel strictement positif :  a > 1,   > 0 ,
lim
x
x
a
x
IV. FONCTIONS TRIGONOMÉTRIQUES DE BASE AVEC COMPLÉMENTS
Notations : Si a, b et  sont des réels ( non nul) , on dit que a et b sont congrus modulo , si et seulement
si a – b est un multiple entier de  et cela se note :
[]ab
. (c’est–à–dire  k  ,
a b k
)
Ainsi, dire que
3[2 ]x
signifie que x peut se mettre sous la forme :
32xk
, k  .

27
1° Fonction sinus
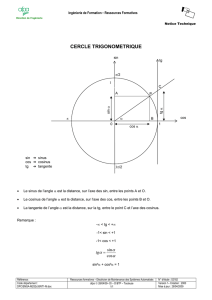
a) Point du cercle trigonométrique : Un point M du cercle trigonométrique étant repéré par l’angle
,i OM
de
mesure x, sin(x) désigne l’ordonnée de M.
b) Équation fondamentale sin(x) = sin() 
[2 ]x
ou
[2 ]x
Cas particuliers essentiels :
sin( ) 0x
0[ ]x
sin( ) 1x
2[2 ]x
sin( ) 1x
2[2 ]x
c) Relations avec angles associés : (formules valables pour tout x réel)
* La fonction sinus est 2 périodique :
sin( 2 ) sin( )xx
*
sin( ) sin( )xx
,
sin( ) sin( )xx
, sin(x + ) = sin(x) et plus généralement,
par récurrence sur n :
n
, sin(x + n) =
( 1)n
sin(x)
d) Valeurs remarquables : sin(
6
) =
1
2
, sin(
4
) =
2
2
, sin(
3
) =
3
2
2° Fonction cosinus
a) Point du cercle trigonométrique : Un point M du cercle trigonométrique étant repéré par l’angle
,i OM
de
mesure x, cos(x) désigne l’abscisse de M.
b) Équation fondamentale cos(x) = cos() 
[2 ]x
ou
[2 ]x
Cas particuliers essentiels :
cos( ) 0x
2[]x
cos( ) 1x
0[2 ]x
cos( ) 1x
[2 ]x
c) Relations avec angles associés : (formules valables pour tout x réel)
* La fonction cosinus est 2 périodique :
cos( 2 ) cos( )xx
*
cos( ) cos( )xx
,
cos( ) cos( )xx
, cos(x + ) = cos(x) et plus généralement,
par récurrence sur n :
n
, cos(x + n) =
( 1)n
cos(x)
d) Valeurs remarquables :
cos(
6
) =
3
2
, cos(
4
) =
2
2
, cos(
3
) =
1
2
.
3° Études croisées de sinus et cosinus
a) Propriétés fonctionnelles de base :
 La fonction sinus est définie sur , impaire, périodique de période 2.
 La fonction cosinus est définie sur , paire, périodique de période 2.
Ces fonctions sont dérivables (donc continues) sur  et :  x  ,
sin ( ) cos( )xx
,
cos ( ) sin( )xx
b) Formules mêlant sinus et cosinus : (formules valables pour tout x réel)
2
sin( ) cos( )xx
et
2
cos( sin( ))xx
(à comparer avec la dérivation...)
2
sin( ) cos( )xx
et
2
cos( sin( ))xx
(échange de sinus et cosinus)
c) Identité circulaire fondamentale :  x   ,
22
sin ( ) cos ( ) 1xx