Scientifique (cours) - Les math. avec H. Rorthais

1e S - programme 2011 - mathématiques – ch.7 - cours Page 1 sur 6
(D’après Hachette - Déclic 2011 – ch.4)
H. Rorthais (Lycée-Collège N.D. de l’Abbaye à Nantes) http://rorthais.math.free.fr
Ch.7 : Etude des variations d’une fonction
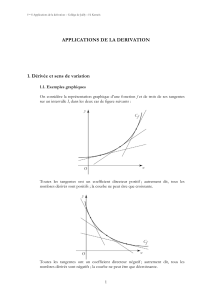
1 SENS DE VARIATION ET OPÉRATIONS SUR LES FONCTIONS
THÉORÈME 1
Somme de fonctions
Soit un réel k et deux fonctions u et v définies sur un intervalle I.
1) Les fonctions u et u + k ont le même sens de variation sur I.
2)
 Si les fonctions u et v sont toutes deux croissantes sur I, alors la fonction u + v est croissante sur I.
 Si les fonctions u et v sont toutes deux décroissantes sur I, alors la fonction u + v est décroissante sur I.
Démonstration :
Voir les démonstrations aux exercices 30 et 31, page 117.
Remarque : (Voir l'exercice 32, page 117)
Si les fonctions u et v n'ont pas le même sens de variation sur l'intervalle I, on ne peut rien conclure sur le sens de
variation de la fonction u + v.
Commentaire :
La courbe représentative de la fonction u + k est l’image de la courbe représentative
de la fonction u par la translation de vecteur k OJ .
THÉORÈME 2
Produit par une constante
Soit un réel  et une fonction u définie sur un intervalle I.
 Si  > 0, alors les fonctions u et u ont le même sens de variation sur I.
 Si  < 0, alors les fonctions u et u, ont des sens de variation contraires sur I.
Démonstration : Cas où  < 0 et u est croissante sur I.
La fonction u conserve l'ordre. Ainsi, pour tous réels a et b dans I tels que a  b, on a : u(a)  u(b).
En multipliant par  (négatif) chaque membre de l'inégalité, on a : u(a) > u(b).
Ainsi la fonction u est décroissante sur I, contrairement à la fonction u.
THÉORÈME 3
 Racine carrée
Soit une fonction u définie sur un intervalle I telle que pour tout réel x de I, u(x)  0.
La fonction u est la fonction définie sur I par : x  u(x).
Les fonctions u et u ont le même sens de variation sur I.
 Inverse
Soit une fonction u définie sur un intervalle I sur lequel u a un signe constant et ne s'annule pas.
La fonction 1
u est la fonction définie sur I par : x  1 u(x) .
Les fonctions u et 1
u ont des sens de variation contraires sur I.
Démonstration :
 Inverse d'une fonction :
Cas où u est croissante et strictement positive sur I.
Pour tous réels a et b dans I tels que a  b, on a : 0 < u(a)  u(b).
La fonction inverse étant décroissante sur ]0 ; +[, on a : 1
u(a)  1 u(b) .

1e S - programme 2011 - mathématiques – ch.7 - cours Page 2 sur 6
(D’après Hachette - Déclic 2011 – ch.4)
H. Rorthais (Lycée-Collège N.D. de l’Abbaye à Nantes) http://rorthais.math.free.fr
Ainsi la fonction 1
u est décroissante sur I, contrairement à la fonction u.
 Voir la démonstration du théorème sur la racine carrée d'une fonction à l'exercice 38, page 118.
Exemple :
Soit f la fonction définie sur IR \ {2} par : f (x) = 1
x – 2 .
On a : f = 1
u où u : x  x – 2.
La fonction u est strictement négative et croissante sur ]– ; 2[.
Donc la fonction f est décroissante sur ]– ; 2[.
De la même façon, la fonction f est décroissante sur ]2 ; +[.
Exercice corrigé : Utiliser les variations des fonctions de référence
On considère les fonctions f, g et h définies sur l'intervalle I :
f (x) = –2x et I = [0 ; +[ ; g(x) = –2x – 3 et I = [0 ; +[ ; h(x) = 1
2x2 + 5 et I = IR.
Étudier les variations de ces fonctions sur leur ensemble de définition.
Solution :
Méthode :
Variations de f :
1) f = (–2)  r où r : x  x.
3) Comme –2 < 0, f et r ont des sens de variation
contraires. Or r est strictement croissante sur
[0 ; +[. Donc f est strictement décroissante sur
[0 ; +[.
4) On vérifie à l'aide de la calculatrice.
1) On cherche une relation
entre la fonction à
étudier et une fonction u,
dont on connaît les
variations.
On conclut en utilisant les
théorèmes du cours.
2) Les fonctions u et v ont le
même sens de variation
dans le cas où :
 v = u + k, où k est
une constante (quel
que soit son signe) ;
 v = u, où  est un
réel strictement
positif ;
 v = u.
3) Les fonctions u et v ont
des sens de variation
contraires dans le cas
où :
 v = u, où  est un
réel strictement
négatif ;
 v = 1
u avec u de signe
constant.
4) Penser à vérifier à l'aide
de la calculatrice : si la
courbe affichée ne
constitue pas une preuve,
c'est un bon élément de
vérification.
Variations de g :
1) On remarque que g = f + (–3).
2) Donc f et g ont le même sens de variation sur
[0 ; +[. Donc la fonction g est strictement
décroissante sur [0 ; +[.
4) On vérifie à l'aide de la calculatrice.
Variations de h :
1) h est l'inverse de la fonction k : x  2x2 + 5, fonction polynôme du second
degré strictement positive sur IR.
Les fonctions h et k ont donc des sens de variation contraires.
Avec les notations habituelles, k change de sens de variation en –b
2a = 0.
Et comme a = 2 (positif), on a le tableau des
variations de la fonction k ci-contre.
3) D'où le tableau des variations ci-contre pour h.
Ainsi h est strictement croissante sur ]– ; 0] et
strictement décroissante sur [0 ; +[.
4) On vérifie à l'aide de la calculatrice.

1e S - programme 2011 - mathématiques – ch.7 - cours Page 3 sur 6
(D’après Hachette - Déclic 2011 – ch.4)
H. Rorthais (Lycée-Collège N.D. de l’Abbaye à Nantes) http://rorthais.math.free.fr
2 SENS DE VARIATION ET DÉRIVATION
THÉORÈME 4
Dérivée d'une fonction monotone
On considère une fonction f définie et dérivable sur un intervalle I.
1) Si f est croissante sur I, alors pour tout réel x de I, f ' (x)  0.
2) Si f est décroissante sur I, alors pour tout réel x de I, f ' (x)  0.
3) Si f est constante sur I, alors pour tout réel x de I, f ' (x) = 0.
Idées de démonstration :
 Cas où la fonction f est constante
Soit une fonction f définie et dérivable sur un intervalle I.
On suppose que f est constante sur I.
Pour tout réel a de I et tout réel h tel que a + h appartient à I,
f (a + h) = f (a), donc le taux d'accroissement de f en a : h  f (a + h) – f (a)
h est la fonction nulle.
Or f ' (a) = lim
h  0 f (a + h) – f (a)
h .
On en déduit que f ' (a) = 0.
 Cas où la fonction f est croissante
Soit une fonction f définie et dérivable sur un intervalle I.
On suppose que f est croissante sur I. Soit un réel a de I.
Pour tout réel h tel que a + h appartient à I :
 Si h > 0, alors a < a + h. f étant croissante sur I, on a : f (a)  f (a + h).
Le rapport f (a + h) – f (a)
h est donc positif.
 Si h < 0, alors a > a + h. f étant croissante sur I, on a : f (a)  f (a + h), donc f (a + h) – f (a)  0.
Et comme h < 0, le rapport f (a + h) – f (a)
h est encore positif.
En passant à la limite quand h tend vers 0, on obtient intuitivement que f ' (a)  0.
Commentaire :
 Si f est croissante sur I, alors en chaque point de la courbe , le coefficient
directeur de la tangente est positif : pour tout réel a de I, f ' (a)  0.
 Si f est décroissante sur I, alors en chaque point de la courbe , le coefficient
directeur de la tangente est négatif : pour tout réel a de I, f ' (a)  0.
THÉORÈME 5
Sens de variation d'une fonction dérivable (admis)
On considère une fonction f définie et dérivable sur un intervalle I.
 Si pour tout réel x de I, f ' (x)  0, alors la fonction f est croissante sur I.
 Si pour tout réel x de I, f ' (x)  0, alors la fonction f est décroissante sur I.
 Si pour tout réel x de I, f ' (x) = 0, alors la fonction f est constante sur I.
Commentaire :
Lorsque la fonction dérivée f ' est de signe constant sur I, et si elle ne s'annule qu'en un nombre fini de valeurs de
I, alors on peut conclure que f est strictement monotone sur I.
Exemple :
Soit la fonction cube f : x  x3.
f est dérivable sur IR et pour tout réel x, f ' (x) = 3x2.
f ' (x) = 0 équivaut à : 3x2 = 0, soit à : x = 0.
Un carré étant positif, pour tout réel x, f ' (x)  0.
Ainsi la dérivée f ' est positive sur IR et ne s'annule qu'en 0. La fonction f est donc
strictement croissante sur IR.

1e S - programme 2011 - mathématiques – ch.7 - cours Page 4 sur 6
(D’après Hachette - Déclic 2011 – ch.4)
H. Rorthais (Lycée-Collège N.D. de l’Abbaye à Nantes) http://rorthais.math.free.fr
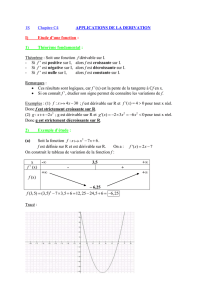
Exercice corrigé : Étudier les variations d'une fonction et choisir une méthode
1) Soit une fonction f dérivable sur [–3 ; 3], dont on donne
la courbe représentative ' de sa dérivée f ' ci-contre.
Étudier les variations de la fonction f.
2) Soit la fonction g définie sur ]0 ; +[ par :
g(x) = 1
x – 2x + 3. Étudier les variations de la fonction g.
3) Soit la fonction h définie sur [0 ; +[ par : h(x) = 1
x + x.
Étudier les variations de la fonction h.
Solution :
1) On lit sur le graphique : f ' s'annule en –2 et en 1, est négative sur
[–3 ; –2] et positive sur [–2 ; 3].
Méthode :
 On déduit les variations de f du
signe de f '.
On résume le signe de f ' (x) dans un tableau de signes.
On en déduit le tableau des variations de f ci-contre.
Remarque : on ne connaît pas les valeurs des images f (–3) ,
f (–2) et f (3) .
2) g est la somme des fonctions x  1
x et de x  –2x + 3, qui sont
 Dans le cas de la somme de
deux fonctions monotones de
même sens de variation, on
peut conclure directement.
 Sinon :
- on calcule f (x) ;
- on étudie le signe de f ' (x) ;
- on en déduit les variations
de f.
 Penser à vérifier à l'aide de la
calculatrice.
 Voir les fiches
Calculatrices, page 394.
toutes deux décroissantes sur
]0 ; +[.
Donc a est décroissante sur
]0 ; +[.
On vérifie à l'aide de la
calculatrice.
3) h est dérivable sur ]0 ; +[ comme somme de fonctions dérivables
sur ]0 ; +[ et pour tout réel x > 0 :
h' (x) = –1
x2 + 1 = –1 + x2 x2 = (x – 1)(x + 1) x2 .
Comme x + 1 et x2 sont strictement positifs, h' (x) est du signe de
(x – 1).
Avec h(1) = 1
1 + 1 = 2.
On vérifie à l'aide de la calculatrice.
3 EXTREMUM D'UNE FONCTION
DÉFINITIONS 1
On considère une fonction f définie sur un intervalle I, et a un réel de I.
 On dit que le réel M est le maximum de f sur I, atteint en a,
si f (a) = M et si pour tout réel x de I, on a f (x)  M.
 On dit que le réel m est le minimum de f sur I, atteint en a,
si f (a) = m et si pour tout réel x de I, on a f (x)  M.
 Un extremum de f sur I est un maximum ou un minimum de f sur I.
 On dit que le réel L est un maximum (respectivement minimum) local de f sur I s'il existe un intervalle
ouvert J contenu dans I, tel que L est le maximum (respectivement minimum) de f sur J.
THÉORÈME 6
Condition nécessaire sur l'existence d'un extremum pour une fonction dérivable (admis)
Soit une fonction f définie et dérivable sur un intervalle I ouvert et a un réel de I.
Si f admet un extremum (local) sur I, atteint en a, alors f ' (a) = 0.

1e S - programme 2011 - mathématiques – ch.7 - cours Page 5 sur 6
(D’après Hachette - Déclic 2011 – ch.4)
H. Rorthais (Lycée-Collège N.D. de l’Abbaye à Nantes) http://rorthais.math.free.fr
Interprétation graphique :
Dans les conditions du théorème précédent, la courbe représentative de f admet en a une tangente parallèle à
l'axe des abscisses.s
Remarques :
 La proposition est fausse dans le cas où I est un intervalle fermé. Sur l'exemple 1 ci-dessous, le maximum de f
est 3, atteint en –5.
Mais la tangente à au point d'abscisse –5 n'a pas pour coefficient directeur 0 : f ' (–5) < 0.
 Cette condition n'est pas suffisante : voir l'exemple 2 ci-dessous.
THÉORÈME 7
Condition suffisante sur l'existence d'un extremum local pour une fonction dérivable
Soit une fonction f définie et dérivable sur un intervalle I ouvert, et a un réel de I.
Si la dérivée f ' s'annule en changeant de signe en a, alors f (a) est un extremum (local) de f sur I.
Idée de démonstration :
Il existe un intervalle ouvert J dans I sur lequel le
tableau de signes de f ', et donc le tableau des
variations de f, est l'un des deux tableaux ci-contre.
Ainsi f (a) est le maximum ou le minimum de la
fonction f sur J.
Exemple 1 :
Sur le schéma ci-contre :
 Le maximum de f sur [–5 ; 3] est 3, atteint en –5.
 Le minimum de f sur [–5 ; 3] est –2, atteint en –3.
 1 est un maximum local de f, car 1 est le maximum de f sur I = ]–2 ; 0[.
 –1 est un minimum local de f, car c'est le minimum de f sur I' = ]0 ; 2[.
Exemple 2 :
Soit la fonction f : x  x3 dérivable sur IR.
Pour tout réel x, f ' (x) = 3x2.
Ainsi f ' (0) = 0.
Mais f étant strictement croissante sur IR, f n'admet pas d'extremum en 0.
Exercice corrigé : Déterminer des extrema, obtenir des inégalités
1) Soit la fonction f définie sur [–7 ; 7] par : f (x) = x
1 + x2 .
Justifier que pour tout réel x de [–7 ; 7] : –1
2  f (x)  1 2 .
2) Démontrer que pour tout réel x  0, on a x3  3x – 2.
Solution :
1) En tant que quotient de fonctions dérivables sur [–7 ; 7] et le
dénominateur ne s'annulant pas, la fonction f est dérivable sur
[–7 ; 7], et pour tout réel x de cet intervalle, on a :
Méthode :
Pour encadrer f (x) :
On peut :
f ' (x) = 1(1 + x2) – x  2x
(1 + x2)2 = 1 – x2 (1 + x2)2 .
 calculer f ' (x) ;
f ' (x) a le signe du trinôme 1 – x2 puisque (1 + x2)2 > 0.
D'où le tableau de signes de f ' (x) et le tableau des variations de f,
 étudier le signe de f ' (x) et en
déduire les variations de f ;