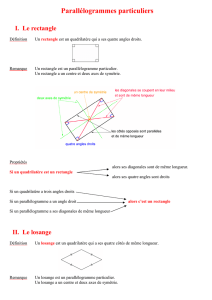
I- Définition:

LE CARRE
I- Définition:
Le quadrilatère ABCD a ses quatre angles droits et ses quatre côtés de
la même longueur
ABCD est un carré
Un carré est un quadrilatère ayant ses quatre angles droits et ses quatre côtés de la même
longueur.
II- Remarque:
Si ABCD un carré, alors:
- (AB) est parallèle à (DC) et(AD) est parallèle à (BC), donc: Tout carré est un
parallélogramme
- ses quatre angles sont droits, donc: Tout carré est un rectangle
- ses quatre côtés sont de la même longueur, donc: Tout carré est un losange
III- Symétries:
Un carré possède:
- quatre axes de symétrie (en vert)
- un centre de symétrie (en rouge)
IV- Propriétés des diagonales:
1) Propriété:
Dans un carré, les diagonales se coupent en leur milieu, sont
perpendiculaires et sont bissectrices des angles
1

V- Montrer qu'un quadrilatère est un carré:
Pour montrer qu'un quadrilatère est un carré, il faut montrer qu'il est à la fois un rectangle et
un losange.
Exemples:
1) Si les diagonales d'un quadrilatère se coupent en leur milieu, sont perpendiculaires et sont
de la même longueur, alors ce quadrilatère est un carré
2) Si les diagonales d'un parallélogramme sont perpendiculaires et de la même longueur, alors
ce parallélogramme est un carré.
3) Si un rectangle a deux côtés consécutifs de la même longueur, alors ce rectangle est un
carré.
4) Si un rectangle a ses diagonales perpendiculaires, alors ce rectangle est un carré.
5) Si un losange a un angle droit, alors ce losange est un carré.
6) Si un losange a ses diagonales de la même longueur, alors ce losange est un carré
VI- Exercices:
Exercice 1:
Montrer que IJKL est un carré
Exercice 2:
Montrer que RSTU est un carré
Exercice 3:
Montrer que DEFG est un carré
Exercice 4:
Montrer que SUVW est un carré
Exercice 5:
Soit PQSR un parallélogramme tel que: PQ = PR et (PQ) ⊥ (PR)
Montrer que PQSR est un carré
2

LE CARRE - CORRECTION DES EXERCICES
Exercice 1:
D'après le codage, IJKL a trois angles droits.
Donc c'est un rectangle car: Si un quadrilatère a trois angles droits, alors ce quadrilatère est un
rectangle.
De plus, d'après le codage: JK = KL
Donc IJKL est un carré car:
Si un rectangle a deux côtés consécutifs de la même longueur, alors ce rectangle est un carré.
Exercice 2:
D'après le codage, (RS) et (UT) sont perpendiculaires à (ST).
Donc (RS) et (UT) sont parallèles car: Si deux droites sont perpendiculaires à une même
droite, alors ces deux droites sont parallèles.
De plus, d'après le codage: RS = UT
Donc RSTU est un parallélogramme car: Si un quadrilatère non croisé a deux côtés parallèles
et de la même longueur, alors ce quadrilatère est un parallélogramme.
Pour la suite, deux méthodes sont possibles:
Méthode 1:
L'angle S (ou l'angle T) est un angle droit.
Donc RSTU est un rectangle car: Si un parallélogramme a un angle droit, alors ce
parallélogramme est un rectangle
De plus RS = RU ( ou RU = UT)
Donc RSTU est un carré car: Si un rectangle a deux côtés consécutifs de la même longueur,
alors ce rectangle est un losange.
Méthode 2:
RS = RU ( ou RU = UT)
Donc RSTU est un losange car: Si un parallélogramme a deux côtés consécutifs de la même
longueur, alors ce parallélogramme est un losange.
De plus l'angle S (ou l'angle T) est un angle droit.
Donc RSTU est un carré car: Si un losange a un angle droit, alors ce losange est un carré
Exercice 3:
D'après le codage O est le milieu de [DF] et de [EG]
Donc DEFG est un parallélogramme car:
Si les diagonales d'un quadrilatère se coupent en leur milieu, alors ce quadrilatère est un
parallélogramme.
Pour la suite, deux méthodes sont possibles:
Méthode 1:
L'angle D est un angle droit.
Donc DEFG est un rectangle car:
Si un parallélogramme a un angle droit, alors ce parallélogramme est un rectangle
3

De plus DE = DG
Donc DEFG est un carré car:
Si un rectangle a deux côtés consécutifs de la même longueur, alors ce rectangle est un
losange
Méthode 2:
DE = DG
Donc DEFG est un losange car:
Si un parallélogramme a deux côtés consécutifs de la même longueur, alors ce
parallélogramme est un losange.
De plus l'angle D est un angle droit.
Donc DEFG est un carré car:
Si un losange a un angle droit, alors ce losange est un carré
Exercice 4:
D'après le codage:
- T est le milieu de [SV] et de [UW]
- SV = WU
- (SV) et (WU) sont perpendiculaires.
Donc SUVW est un carré car:
Si les diagonales d'un quadrilatère se coupent en leur milieu, sont perpendiculaires et sont de
la même longueur, alors ce quadrilatère est un carré
Exercice 5:
On obtient la figure ci-dessous: Deux méthodes de démonstration sont possibles.
Méthode 1:
L'angle P est un angle droit.
Donc PQSR est un rectangle car:
Si un parallélogramme a un angle droit, alors ce
parallélogramme est un rectangle
De plus PQ = PR
Donc PQSR est un carré car:
Si un rectangle a deux côtés consécutifs de la même
longueur, alors ce rectangle est un losange.
Méthode 2:
PQ = PR
Donc est un losange car:
Si un parallélogramme a deux côtés consécutifs de la même
longueur, alors ce parallélogramme est un losange.
De plus l'angle P est un angle droit.
Donc PQSR est un carré car:
Si un losange a un angle droit, alors ce losange est un carré
4