temps a bord vaisseau spatial

ACCUEIL
Relativité :
Temps à bord d’un vaisseau spatial uniformément accéléré
Frédéric Élie, 27/2/2004
La reproduction des articles, images ou graphiques de ce site, pour usage collectif, y compris dans le cadre des études scolaires et
supérieures, est INTERDITE. Seuls sont autorisés les extraits, pour exemple ou illustration, à la seule condition de mentionner
clairement l’auteur et la référence de l’article.
Vous connaissez peut-être le paradoxe des jumeaux du physicien français Paul
Langevin, en rapport avec les conséquences prévues par la relativité restreinte
d'Einstein sur la contraction de la durée? Dans ce paradoxe un astronaute qui quitterait
la Terre pour aller quelque part dans la galaxie, puis qui reviendrait sur notre planète, ne
retrouverait pas vivant son frère jumeau resté sur elle: plusieurs décennies se seraient
écoulées sur la Terre, tandis que pour l'astronaute à bord de sa fusée, la durée du
voyage aurait été seulement de quelques années. Dans le paradoxe des jumeaux on
admet que la vitesse de la fusée reste constante. En fait, pour tenir compte du fait que
cette fusée part puis revient vers la Terre, il faut considérer que sa vitesse est
uniformément croissante jusqu'à sa destination (accélération uniforme), puis
uniformément décroissante jusqu'à s'annuler sur Terre pour le chemin du retour
(décélération uniforme). La question abordée ici est de savoir ce que devient le paradoxe
des jumeaux pour le cas d'une fusée accélérée et décélérée?…
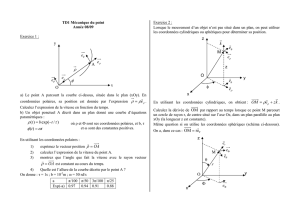
Une fusée est uniformément accélérée sur une distance 0 à D/2 puis uniformément décélérée
(de la même grandeur G) entre D/2 et D.
Le calcul montre (cf ci-dessous) que si l’accélération est choisie égale à celle de la pesanteur
(pour des raisons de viabilité à bord) G = g, on peut parcourir le diamètre de la galaxie (100 000
années lumière) en une génération (20 ou 30 ans)
©Frédéric Élie, 27 février 2004 - http://fred.elie.free.fr - page 1/4
Mais la difficulté est de trouver un moyen de propulsion capable d’imprimer une accélération
égale à g pendant cette période : aucune source d’énergie classique embarquable ne le permet
!
Calcul théorique
du temps passé à bord en fonction de la distance parcourue
(formule de Peschka et Sanger)
Le référentiel propre de la fusée (x’, t’) s’éloigne du référentiel fixe de la terre (x, t) avec une
vitesse v = dx /dt = dx’/dt’. Dans le référentiel fixe le quadrivecteur est :
dx = (cdt, dx, 0, 0)
le temps propre (dans la fusée) dt’ est tel que :
avec v = dx/dt = dx’/dt’ et donc
quadrivitesse dans le référentiel fixe :
©Frédéric Élie, 27 février 2004 - http://fred.elie.free.fr - page 2/4
quadri-accélération dans le référentiel fixe :
or dans le référentiel mobile (propre) l’accélération est la dérivée par rapport au temps propre
de la vitesse propre :
wi = (0, d/ds (dx’/ds), 0, 0) = (0, d/ds (dx’/cdt’), 0, 0) = (0, 1/c² dv/dt’, 0, 0) = (0, G/c², 0, 0) avec G
= dv/dt’
l’accélération étant un invariant on a :
c’est-à-dire :
qui s’intègre pour donner la vitesse :
On en déduit le temps propre dans la fusée :
Soit
©Frédéric Élie, 27 février 2004 - http://fred.elie.free.fr - page 3/4
qui s’intègre en :
où t est la durée du voyage jusqu’à mi-chemin D/2 (accélération croissante uniforme) ; pour la
totalité du trajet on a :
mais l’accélération étant constante on a la loi horaire : D/2 = ½ Gt² jusqu’à mi-chemin donc
On a, de façon équivalente :
ce qui pour de faibles valeurs de l’accélération donne la formule de Peschka et Sanger :
Si, par exemple, vous avez mis 27 années à bord du vaisseau pour parcourir un million
d'années lumière, à raison d'une accélération de 1g, combien d'années se sont écoulées sur
Terre? Le calcul donne 984 années écoulées sur Terre! Si vous êtes partis à l'époque où
régnait en France le roi capétien Robert II Le Pieux, vous reviendrez fêter la nouvelle année
2004 avec vos descendants d'une trentaine de générations !!!
faites le calcul vous-même !
contraction du temps dans un vaisseau accéléré
BIBLIOGRAPHIE
W. Peschka: Astronautica Acta (vol. II, 1956, p. 191)
E. Sänger: Astronautica Acta (vol. III, 1957, p. 89)
L. Landau, E. Lifchitz: théorie des champs, éd. Mir, Moscou, 1970
©Frédéric Élie, 27 février 2004 - http://fred.elie.free.fr - page 4/4