Sujet

TS – Physique-Chimie Evaluation type bac
Page 1 sur 6
Exercice I : ACIDE LACTIQUE ET MÉDECINE ANIMALE (7 points)
Des tests d’effort sont pratiqués par des vétérinaires afin d’évaluer la condition physique des
chevaux. Celle-ci est liée à l’apparition d’acide lactique dans les muscles pouvant entraîner des
crampes douloureuses après un exercice physique prolongé. L’acide lactique est également à la base
de la fabrication d’un polymère biodégradable, l’acide polylactique, utilisé en chirurgie vétérinaire
pour réaliser des sutures.
Les parties 1, 2 et 3 sont indépendantes.
1. L’acide lactique
La formule semi-développée de l’acide lactique est la suivante : H
3
C − CH − C
1.1. Étude de la molécule d’acide lactique
1.1.1. Donner la formule topologique de cet acide.
1.1.2. Entourer sur la représentation précédente les groupes caractéristiques présents dans la
molécule et les nommer.
1.2. Analyse spectroscopique
1.2.1. Parmi les spectres IR proposés dans le document 1 ci-après, choisir en justifiant celui
correspondant à l’acide lactique.
1.2.2. Prévoir, en justifiant la réponse, le nombre de signaux présents dans le spectre RMN de
l’acide lactique ainsi que leur multiplicité.
Donnée : bandes d’absorption en spectroscopie IR
Document 1 : Spectres IR
Spectre IR n°1
Liaison
C−C
C=O
O
−
H (acide
carboxylique)
C−H
O
−
H
(alcool)
Nombre
d’onde (cm
−1
)
1000 - 1250 1700 - 1800
2500 - 3200 2800 - 3000 3200 - 3700
O
OH
OH
TS – Physique-Chimie Evaluation type bac
Page 2 sur 6
Spectre IR n°2
2. Test d’effort d’un cheval
Le test d’effort d’un cheval est constitué de plusieurs phases. Durant chacune d’elles, le cheval se
déplace à une vitesse constante qui est augmentée d’une phase à l’autre et on mesure sa fréquence
cardiaque ainsi que sa vitesse. Une prise de sang est effectuée à l’issue de chaque temps d’effort afin
de doser l’acide lactique.
Donnée : masse molaire de l’acide lactique : 90,0 g.mol
−
1
2.1. Dosage de l’acide lactique après une phase du test
Le cheval court durant trois minutes à la vitesse de 500 m/min. Un vétérinaire prélève ensuite sur ce
cheval un volume V = 1,00 mL de sang dont il extrait l’acide lactique. Cet acide est dissous dans l’eau
pour obtenir une solution S de volume V
S
= (50,00 ± 0,05) mL.
Il réalise le dosage de la totalité de cette solution S par une solution aqueuse d’hydroxyde de sodium
Na
+(aq)
+ HO
−(aq)
de concentration molaire C
1
= (1,00 ± 0,01) × 10
−3
mol.L
−1
. L’équivalence est
obtenue pour un volume de solution d’hydroxyde de sodium ajoutée V
E
= (4,0 ± 0,4) mL.
2.1.1. Écrire l’équation de la réaction support du dosage en utilisant la notation AH pour l’acide
lactique.
2.1.2. Exprimer la concentration molaire C
S
en acide lactique de la solution S puis calculer sa valeur.
L’incertitude relative d’une grandeur X est définie par le rapport
X
X
∆
.
On admet qu’une incertitude relative est négligeable devant une autre, si elle est environ dix fois plus
petite. Dans l’hypothèse où les incertitudes relatives sur V
S
et C
1
sont négligeables devant celle sur
V
E
, on admet que l’incertitude relative
S
S
C
C
∆
=
E
E
V
V
∆
.

TS – Physique-Chimie Evaluation type bac
Page 3 sur 6
2.1.3. Déterminer l’encadrement de la concentration molaire en acide lactique C
S
obtenue par le
vétérinaire.
2.1.4. En déduire l’encadrement de la concentration molaire C en acide lactique dans le sang du
cheval.
2.2. Évaluation de la condition physique du cheval
Le cheval a subi un test similaire trois semaines auparavant.
À l’aide des documents 2 et 3, déterminer si le cheval examiné par le vétérinaire est actuellement en
meilleure forme que trois semaines auparavant.
Donnée : Pour une vitesse donnée, un cheval est d’autant plus performant que la concentration en
acide lactique de son sang est faible.
Document 2 : Concentration massique en acide lactique à l’issue de différentes phases d’un test
d’effort en fonction de la vitesse, pour un test réalisé trois semaines auparavant.
Document 3 : « paramètre V4 »
Le « paramètre V4 » est défini par la valeur de la vitesse qui correspond à une concentration en acide
lactique de 0,36 g.L
−1
. Ce paramètre est assimilable à un seuil de fatigue. Il dépend de l’âge du cheval,
de son niveau d’entraînement et de sa capacité individuelle à l’effort.
D’après http://pegase.mayenne.
0
0,1
0,2
0,3
0,4
0,5
0,6
0,7
0,8
0,9
1
0 100 200 300 400 500 600 700 800
concentration massique en acide
lactique (g/L)
vitesse (m/min)
TS – Physique-Chimie Evaluation type bac
Page 4 sur 6
3. Polymérisation de l’acide lactique
Une molécule d’acide lactique peut, dans certaines conditions, réagir avec une autre molécule d’acide
lactique pour former une molécule de chaîne plus longue, à six atomes de carbone. À son tour cette
dernière peut réagir avec une autre molécule d’acide lactique pour donner une molécule encore plus
longue et ainsi de suite. On obtient ainsi une molécule de polymère constituée d’un très grand
nombre d’atomes de carbone, appelée acide polylactique, reproduisant régulièrement le même motif
d’atomes. L’acide polylactique est un polymère biodégradable : l’action de l’eau peut le détruire en
régénérant l’acide lactique.
Document 4 : Protocole de synthèse de l’acide polylactique
- Introduire environ 10 mL d’acide lactique pur dans un bécher.
- Ajouter délicatement quelques gouttes d’acide sulfurique à l’aide de gants et de lunettes de
protection.
- Chauffer à 110°C en agitant régulièrement.
- Au bout d’environ trente minutes, laisser refroidir le mélange qui se solidifie mais reste
transparent : il s’agit de l’acide polylactique.
D’après http://www.ac-nancv-metz.fr/
3.1. La polymérisation de l’acide lactique est-elle lente ou rapide ? Justifier.
3.2. Citer un paramètre influençant l’évolution temporelle de cette réaction chimique.
3.3. Proposer un protocole permettant de vérifier que l’acide sulfurique est un catalyseur de cette
réaction.

TS – Physique-Chimie Evaluation type bac
Page 5 sur 6
EXERCICE II. LES TIRS AU BUT (6 points)
Antonin PANENKA, footballeur international tchécoslovaque est connu pour avoir laissé son nom à
une technique particulière pour tirer les penaltys ou « tirs au but ». Au lieu de frapper en force, il
frappe doucement le ballon qui prend alors une trajectoire en « cloche ». Son geste est devenu
célèbre au soir de la finale de la Coupe d’Europe des Nations de 1976, où la Tchécoslovaquie battait
la République Fédérale d’Allemagne tenante du titre. Antonin PANENKA marquant le dernier pénalty
par cette technique de balle « en cloche » venait d’inventer la « Panenka ».
Lors d’un match de football, un joueur doit tirer un pénalty et décide
de tenter une « Panenka ». Le joueur dépose le ballon au point de
pénalty O, pris comme origine du repère.
Le joueur tape le ballon en direction du centre du but et lui
communique une vitesse initiale
0
v
uur
de valeur 11,5 m.s
-1
et dont la
direction fait un angle α = 55° avec l’horizontale.
Données :
• intensité de la pesanteur : g = 9,81 N.kg
-1
;
• masse du ballon : m = 620 g ;
• termes utilisés dans la pratique du football :
Les buts
Les buts sont constitués de deux montants verticaux (poteaux) reliés en leur sommet par une barre
transversale. Le bord inférieur de la barre transversale se situe à une hauteur de 2,44 m par rapport
au sol.
Le pénalty
Le pénalty est une action consistant à frapper directement au but depuis un point nommé « point de
pénalty » ou « point de réparation ». Un pénalty est réussi si le ballon franchit la ligne de buts en
passant entre les montants et sous la barre transversale.
La surface de réparation
À l’intérieur de chaque surface de réparation, le point de pénalty est marqué à 11,0 m du milieu de la
ligne de but et à égale distance des montants verticaux du but.
1. Schématisation du problème
1.1. Tracer un repère orthonormé (Ox, Oz) et représenter, dans ce repère, la situation du pénalty,
sans souci d’échelle.
Les grandeurs suivantes devront apparaitre : le vecteur vitesse initiale
0
v
uur
, l’angle α ; la hauteur h
des buts et la distance d du point de pénalty à la ligne de but.
1.2. On note A le point où se situe le ballon lorsqu’il franchit la ligne de but. Quelles conditions
doivent vérifier les coordonnées (x
A
; z
A
) de ce point pour que le pénalty soit réussi ?
TS – Physique-Chimie Evaluation type bac
Page 6 sur 6
2. Étude dynamique du mouvement du ballon
Dans cette partie, on étudie le mouvement du centre d’inertie G du ballon en négligeant les forces de
frottement de l’air sur le ballon ainsi que la poussée d’Archimède.
2.1. Établir l’expression du vecteur accélération
G
a
uur
du centre d’inertie du ballon.
2.2. Établir les équations horaires x(t) et z(t) du mouvement du centre d’inertie G et montrer que
l’équation de la trajectoire du ballon, dans le plan (xOz), peut s’écrire :
2
0
. ²
( ) tan .
2. .(cos )²
g x
z x x
v
= − + α
α
2.3. En exploitant les données et les documents, déterminer si le pénalty décrit en début d’exercice
est réussi. Expliciter votre raisonnement.
3. Étude énergétique du mouvement du ballon
On admet que le ballon passe au niveau de la ligne de but à une hauteur z
A
= h
A
.
3.1. Rappeler les expressions de l’énergie cinétique E
c
, de l’énergie potentielle de pesanteur E
pp
et de
l’énergie mécanique E
m
. On choisira un axe vertical ascendant et une énergie potentielle de
pesanteur nulle à l’origine.
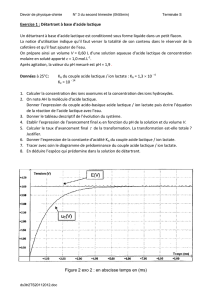
En explicitant votre raisonnement, associer à chaque courbe du document 1 la forme d’énergie
correspondante.
3.2. À l’aide du document 1, déterminer les valeurs de la hauteur h
A
et de la vitesse v
A
lorsque le
ballon franchit la ligne de but.
3.3. Que peut-on dire de l’énergie mécanique du ballon lors de son mouvement ? Utiliser cette
caractéristique du mouvement pour retrouver la valeur v
A
de la vitesse du ballon lorsqu’il franchit la
ligne de but et comparer le résultat trouvé avec celui de la question 3.2. Conclure.