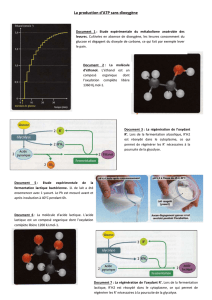
exercice 1 - Site Gerald VINCENT

Devoir de physique-chimie N° 3 du second trimestre (0h55min) Terminale S
ds3tr2TS20112012.doc
Exercice 1 : Détartrant à base d’acide lactique
Un détartrant à base d’acide lactique est conditionné sous forme liquide dans un petit flacon.
La notice d’utilisation indique qu’il faut verser la totalité de son contenu dans le réservoir de la
cafetière et qu’il faut ajouter de l’eau.
On prépare ainsi un volume V = 0,60 L d’une solution aqueuse d’acide lactique de concentration
molaire en soluté apporté c = 1,0 mol.L-1.
Après agitation, la valeur du pH mesuré est pH = 1,9 .
Données à 25°C: KA du couple acide lactique / ion lactate : KA = 1,3  10 - 4
Ke = 10 - 14
1. Calculer la concentration des ions oxoniums et la concentration des ions hydroxydes.
2. On note AH la molécule d’acide lactique.
Donner l’expression du couple acido-basique acide lactique / ion lactate puis écrire l’équation
de la réaction de l’acide lactique avec l’eau.
3. Donner le tableau descriptif de l’évolution du système.
4. Etablir l’expression de l’avancement final xf en fonction du pH de la solution et du volume V.
5. Calculer le taux d’avancement final de la transformation. La transformation est-elle totale ?
Justifier.
6. Donner l’expression de la constante d’acidité KA du couple acide lactique / ion lactate.
7. Tracer avec soin le diagramme de prédominance du couple acide lactique / ion lactate.
8. En déduire l’espèce qui prédomine dans la solution de détartrant.
Figure 2 exo 2 : en abscisse temps en (ms)

Devoir de physique-chimie N° 3 du second trimestre (0h55min) Terminale S
ds3tr2TS20112012.doc
Exercice 2 Etude expérimentale d’un dipôle « résistance et condensateur en série »
Pour étudier ce dipôle, on réalise le circuit représenté sur la figure 1.
Ce circuit est constitué d’un générateur idéal de tension continue de force électromotrice E, d’un
interrupteur K, d’un conducteur ohmique de résistance R et d’un condensateur de capacité C.
Données : E = 4,0 V ;
C = 1,0 µF
On utilise une interface d’acquisition reliée à un ordinateur pour observer les tensions uC et E en fonction
du temps (figure 2 page précédente).
1. Représenter sur la figure 1 les flèches de tension E, uR et uC.
2. À quels points A, B, D ou M du circuit doit-on relier les voies 1 et 2 et la masse de l’interface
pour visualiser uC sur la voie 1 et E sur la voie 2 ? Représenter ces trois connexions sur la figure 1.
À t = 0, on déclenche l’acquisition en fermant l’interrupteur K.
Les courbes uC = f(t) et E = f(t) sont données sur la figure 2 page précédente.
3. Qualifier les deux régimes de fonctionnement du circuit en choisissant parmi les adjectifs
suivants : périodique, permanent, pseudo-périodique, transitoire.
Préciser les dates limitant chacun de ces régimes.
Quel phénomène physique se produit pendant le premier régime ?
4. La constante de temps  est une caractéristique de ce premier régime.
Déterminer graphiquement la valeur de  en expliquant la méthode employée.
Donner l’expression littérale de  en fonction des caractéristiques des éléments du circuit.
En déduire la valeur de la résistance R.
5. En appliquant la loi d’additivité des tensions, donner la relation littérale liant E, uR et uC.
6. Etablir alors l’équation différentielle du premier ordre qui régit l’évolution de uc au cours du
temps.
De quelle forme mathématique (détailler les termes) est la solution de cette équation (aucune
résolution n’est demandée) ?
7. Exprimer uR en fonction de i et en déduire une expression littérale de l’intensité du courant i en
fonction de E, uC et R.
8. À l’aide de la figure 2 page précédente, calculer i pour t1 = 0 ms et t2 = 9 ms.
Sans considération d’échelle, en déduire sur votre copie l’allure de la courbe i = f(t).
Figure 1
uR
E
M
uC
C
D
A
R
K
B
i

Devoir de physique-chimie N° 3 du second trimestre (0h55min) Terminale S
ds3tr2TS20112012.doc
Exercice 1 : Détartrant à base d’acide lactique
1. [H3O+(aq)]eq = 10-pH = 1,3×10–2 mol.L- 1 et Ke = [OH-]eq × [H3O+]eq => [OH-]eq = 7,9×10–13 mol.L- 1
2. couple: AH / A– et AH(aq) + H2O(l) = A–(aq) + H3O+(aq)
3.
Équation chimique
AH(aq) + H2O(l) = A–(aq) + H3O+(aq)
État du
système
Avancement (mol)
Quantités de matière (mol)
État initial
x = 0
c.V
Excès
0
0
État final
=equilibre
xf
c.V – xf
Excès
xf
xf
4. dans le tableau on voit que xf = n(H3O+(aq))f donc xf = [H3O+(aq)]f.V donc xf = 10–pH.V
5. Si la transformation est totale, le réactif limitant AH est entièrement consommé :
donc c.V – xmax = 0 donc xmax = c.V
Alors
pH
f
max
x10 .V
x c.V
donc
pH
10c
calcul :
1,9
101
= 1,3×10–2 = 1,3 % :  est inférieur à 100%, la transformation n’est pas totale.
6. Constante d’acidité de l’acide lactique KA =
3
eq eq
eq
A . H O
AH
7. Diagramme :
8. pH<pKA donc l’espèce qui prédomine dans la solution de détartrant est AH(aq).
Exercice 2
1. voir dessin ci contre : uR et uC convention
recepteur, E convention générateur
2. Masse au point M,
Voie 1 au point D
Voie 2 au point A
On mesure ainsi les tensions:
uC = uDM aux bornes du condensateur,
E = uAM aux bornes du générateur.
Voie 2
Voie 1

Devoir de physique-chimie N° 3 du second trimestre (0h55min) Terminale S
ds3tr2TS20112012.doc
3.
Régime transitoire : la tension uC(t)
augmente entre t = 0 et t = 6,0 ms.
Régime permanent : la tension uC(t) est
constante et égale à E = 4,00 V, à partir de t
= 6,0 ms.
Durant le régime transitoire, il se produit la
charge du condensateur.
4. Méthode des 63% :
Pour t =  , uC() = 0,63 x E = 0,63 x 4,00 = 2,52 V  2,5 V
On trace la droite uc() = 2,5 V ; cette droite coupe le graphe uC(t) en un point d’abscisse égale à 
On peut aussi utiliser la méthode de la tangente à l’origine !
 = R.C donc Erreur ! Des objets ne peuvent pas être créés à partir des codes de champs de mise en
forme. donc Erreur ! Des objets ne peuvent pas être créés à partir des codes de champs de mise en
forme.= 1,0.103  = 1,0 k.
5. Loi d’additivité des tensions : E = uR(t) + uC(t)
6. Démonstration du cours
C.RE
u
C.R1 dt
ud C
C
solution :
t
c
u t A B e
où A et B constantes, t le temps et  = R.C
7. Loi d’Ohm (convention récepteur) : uR(t) = R.i(t) Donc : E = R.i(t) + uC(t)  i(t) = Erreur ! Des objets
ne peuvent pas être créés à partir des codes de champs de mise en forme.
8. Pour t1 = 0 ms, uC(t1) = 0 V donc : i(t1) = Erreur ! Des objets ne peuvent pas être créés à partir des
codes de champs de mise en forme.= 4,0.10–3 A = 4,0 mA.
Pour t2 = 9 ms, uC(t2) = E = 4,0 V donc : i(t2) = Erreur ! Des objets ne peuvent pas être créés à partir des
codes de champs de mise en forme.= 0 .
Allure du graphe i(t) : l’intensité décroît
exponentiellement de 4,0 mA jusqu’à tendre vers 0 A.
i(m
A)
t(ms)
4,0
0
9
Régime transitoire
Régime permanent