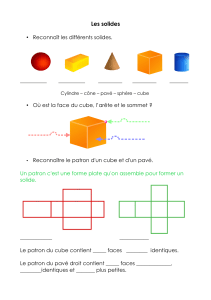
7. Fiche Leçon Pavées droits et cubes

PARALLÉLÉPIPÈDES RECTANGLES ET CUBES
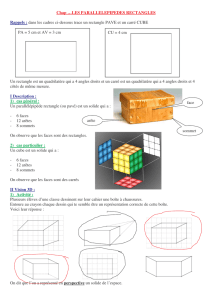
I. DESCRIPTION DU PARALLÉLÉPIPÈDE RECTANGLE
a. Les arêtes
Les arêtes d’un parallélépipède rectangle sont les côtés de ses faces
(ce sont les « bords » du parallélépipède).
Propriété Un parallélépipède rectangle a 12 arêtes
.
b. Les faces opposées
Deux faces d’un parallélépipède rectangle qui n’ont pas d’arête en
commun sont opposées.
Propriété
Deux faces opposées d’un parallélépipède rectangle sont des rectangles
superposables Les faces grisées sont deux faces opposées.
c. Les sommets
Les « coins » d’un parallélépipède rectangle peuvent être vus comme
les sommets des rectangles : on les appelle aussi les sommets du
parallélépipède rectangle.
Propriété Un parallélépipède rectangle a 8 sommets En rouge : les 8 sommets.
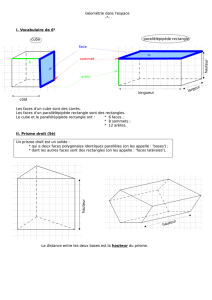
II. LE CUBE
Toutes les arêtes d’un parallélépipède rectangle peuvent avoir la même longueur : toutes les faces
sont alors des carrés.
Définition : Un cube est un parallélépipède rectangle dont les faces sont des carrés.
III. PATRONS D’UN PARALLÉLÉPIPÈDES RECTANGLES
Un patron d’un solide est une figure plane qu’on pourrait obtenir par dépliage de ce solide.
Inversement, à partir d’un patron d’un solide, on peut fabriquer ce solide par pliage.
A. Patrons d’un parallélépipède rectangle
On peut imaginer que l’on déplie le parallélépipède rectangle.
Il y a plusieurs patrons possibles pour un même parallélépipède rectangle, cela dépend de la façon dont on le
déplie !
Pour n’importe quel parallélépipède rectangle :
• un patron est formé de 6 rectangles ;
• les rectangles d’un patron correspondant à des faces opposées sur le solide ont les mêmes dimensions ;
• les côtés des rectangles qui coïncident lors du pliage ont la même longueur.

B. Patrons d’un cube
Les patrons d’un cube sont formés de 6 carrés de même côté.
Un même cube vu de deux
façons différentes
Un patron du cube Un autre patron du cube
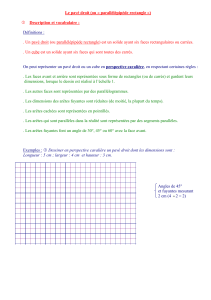
IV. PARALLÉLÉPIPÈDES RECTANGLES ET PERSPECTIVES CAVALIÈRES
La perspective cavalière permet de représenter sur une feuille des solides de l’espace.
Les arêtes de la même couleur sont
parallèles et de la même longueur.
Deux faces opposées sont parallèles.
En perspective cavalière :
Des segments parallèles dans la réalité sont représentés par des segments parallèles.
Deux arêtes ayant un sommet commun sont
perpendiculaires.
Deux faces ayant une arête commune sont des
faces perpendiculaires.
En perspective cavalière :
Des angles droits dans la réalité ne sont pas toujours représentés par des angles droits.
Seules les faces de devant et de derrière ne sont pas déformées : elles sont représentées par des rectangles en
vraie grandeur.
Exemple :
J est le milieu de [AD]
sur la représentation
comme dans la
réalité.
Sur la représentation :
• la longueur FG est plus courte que
la longueur réelle ;
• les longueurs dans les faces de
devant et de derrière sont
en vraie grandeur.