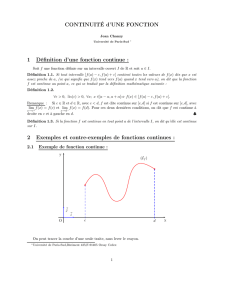
Chapitre 12 - Pierre

f:Df⊂R→R
a∈R

f:Df−→ RDf⊂R
a∈R
f a a ∈Df
f a lim
x→af(x) = f(a).
a
f(a) lim
x→af(x) = 6=f(a)
f a f(a)f
a f(x) = 1
x0
f a
∀ε > 0,∃α>0,∀x∈Df,|x−a|<α=⇒ |f(x)−f(a)|< ε.
a
a= 1 f(x) = 
x2−4
x−2x6= 1
3x= 1.
a= 0 f(x) = 
e−1
x2x6= 0
1x= 0.

a=−1f(x) = 
ln |x|x6=−1
5x=−1.
f a a ∈Dff
•alim
x→
<af(x) = f(a).
•alim
x→
>af(x) = f(a).
f(x) = bxc2
k∈Z
f a
f a f a

f(x) = 
e−1
|x|x6= 0,
0x= 0.f x = 0
f(x) = 
e−1
xx6= 0,
0x= 0.f x = 0
I f I \ {a}
lim
x→af(x) = ∈RI
g:I−→ R
x7−→ 
f(x)x6=a
 x =a.
g a
f a
f:R∗−→ R
x7−→ ex−1
x
I J

IRf:I→R
f I f a I
P(x)
P(x)/Q(x)
|x|
ln x
ex
xαx1/2=√x
[n;n+ 1[ n∈Z
n
lim
x→2√x=. . . lim x→3ex=. . . lim x→1ln(x) = . . .
f:I→Rg:I→R∀λ∈R
 λ λf I
 f +g I
 fg I
 g f
gI