S2.2 - TSI Ljf.html

Informatique Cours S2.2 Intégration numérique
Lycée Jules Ferry Cannes Page 1 sur 3 TSI1
L'intégration numérique d'une fonction  →  (où x et f(x) sont 2 nombres) est obtenue en calculant
l'aire sous la courbe par discrétisation de l'intervalle des abscisses (partition de l'intervalle avec un pas
constant à priori). On utilise les valeurs de la fonction aux bornes de la partition pour évaluer l'aire sous la
courbe.
Les algorithmes d'intégration numérique doivent être connus.
1 Méthode des rectangles
1.1 Rectangles à gauche
La méthode d'intégration par les rectangles à gauche consiste à
assimiler l'aire sous la courbe de la fonction à la somme des
rectangles de chaque partition.
La hauteur du rectangle d'une partition vaut la valeur de
la fonction à gauche de la partition.
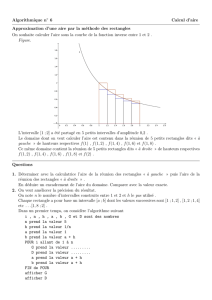
Algorithme d'intégration numérique par la méthode des rectangles
""" Paramètres d'entrées :
*f* : fonction à intégrer (cette fonction renvoie un nombre)
*a* et *b* : début et fin de l'intervalle d'intégration (flottants ou entiers)
*N* : nombre de partitions de l'intervalle d'intégration (entier)
Sortie : intégrale numérique par la méthode des rectangles
"""
- en pseudo code :
Algorithme d'intégration par les rectangles à gauche
h←(b-a)/N # pas des partitions
s←0 # initialisation de la somme
Pour k variant de 0 à N-1 faire # somme de l'aire des rectangles de toutes les partitions
s←s + h*f(a+k*h) # rectangle de hauteur = valeur de la fonction à gauche de la partition
Fin Pour
Fin de l'algorithme d'intégration par les rectangles à gauche
- en python :
def rectangleg(f,a,b,N): 1
h=(b-a)/N # pas des partitions 2
s=0 # initialisation de la somme 3
for k in range(N): # somme de l'aire des rectangles de toutes les partitions 4
s=s + h*f(a+k*h) # rectangle de hauteur = valeur de la fonction à gauche de la partition 5
return s
6
Exemple d'utilisation de la fonction : integ_cos = rectangleg (cos, 0, pi/2, 100)
Les principales capacités
développées sont :
• comprendre un algorithme et expliquer ce qu’il fait,
• modifier un algorithme existant pour obtenir un résultat différent,
• concevoir un algorithme répondant à un problème précisément posé,
• expliquer le fonctionnement d’un algorithme,
• s’interroger sur l’efficacité algorithmique temporelle d’un algorithme.
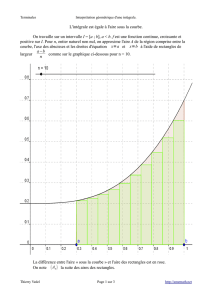
Figure
1
: intégration numérique (rectangles à gauche).

Informatique Cours S2.2 Intégration numérique
Lycée Jules Ferry Cannes Page 2 sur 3 TSI1
1.2 Rectangles à droite
Il s'agit de calculer l'aire des rectangles en prenant comme hauteur du
rectangle d'une partition la valeur de la fonction à droite de la partition.
Seule la ligne 5 change : s = s + h * f(a+(k+1)*h)
1.3 Intérêt de l'intégration par la méthode des rectangles.
A partir des figures précédentes, on comprend que l'erreur de l'intégration numérique se réduit en
augmentant le nombre N de partitions.
Encadrement de l'erreur par les méthodes des rectangles
Pour une fonction croissante (ou décroissante), l'intégrale effective de la fonction est comprise entre
l'intégrale numérique par les rectangles à gauche et celle par les rectangles à droite.
Cela permet en combinant les 2 méthodes d'avoir un majorant de l'erreur réalisée par l'intégration
numérique pour une partition en N morceaux. Par contre il convient de vérifier que la fonction est monotone
sur l'intervalle.
Il faut déterminer la dérivée de la fonction par dérivation numérique
∗∗
puis vérifier
que la dérivée reste positive (ou négative). On peut éventuellement fractionner l'intervalle [a,b] par
morceaux où f est monotone.
Encadrement de l'erreur par la majoration de la dérivée
On montre par ailleurs (cours de mathématiques) que l'erreur par l'intégration numérique est majorée par
max
| |∗
 – 
 si f : fonction continue, dérivable et de dérivée continue sur [a,b].
Pour déterminer ce majorant de l'erreur, il convient de déterminer la dérivée de la fonction puis son
maximum (en valeur absolue).
Cette expression du majorant nous montre qu'en augmentant N on diminue l'erreur d'un facteur 1/N .
L'algorithme dont la précision est inversement proportionnelle à N est dit d'ordre 1.
Seuil de précision E
Pour les 2 cas de majoration, on peut déterminer le nombre de partition N permettant d'obtenir une
intégration numérique avec une erreur inférieure à un seuil de précision E :
- encadrement par les 2 méthodes des rectangles : on fait croitre N jusqu'à atteindre la précision E ou
- si f est dérivable et f' continu : calcul de N à partir du majorant de f'(x) et de l'erreur maximum
attendue :  = max
≤≤!"#
′
#%
∗
! – 
2
2' .
Figure
2
: intégration numérique (rectangle à droite).

Informatique Cours S2.2 Intégration numérique
Lycée Jules Ferry Cannes Page 3 sur 3 TSI1
2 Méthode des trapèzes
On observe en comparant la Figure 1 et la Figure 3 que la méthode d'intégration à partir de l'aire des
trapèzes réduit l'écart par rapport l'intégrale de la courbe
continue.
Seul le calcul de l'aire change dans l'algorithme
d'intégration. L'aire d'un trapèze est sa hauteur h multipliée
par la moyenne de ses bases f(a+k*h) et f(a+(k+1)*h).
La ligne 5 devient ainsi :
s = s + h* ( f(a+k*h) + f(a+(k+1)*h) ) / 2
Encadrement de l'erreur par la majoration de la dérivée seconde
On montre (cours de mathématiques) que l'erreur par l'intégration numérique est majorée par
E= max
| |∗
 – 
(
)∗
si f est une fonction continue, 2 fois dérivable et de dérivées continues sur [a,b].
Pour déterminer ce majorant de l'erreur, il convient de déterminer les dérivées de la fonction puis le
maximum de la dérivée seconde (en valeur absolue).
Cette expression du majorant nous montre qu'en augmentant N on diminue l'erreur d'un facteur 1/N² .
L'algorithme dont la précision est inversement proportionnelle à N² est dit d'ordre 2.
Optimisation de N pour les fonctions non régulière
Pour optimiser N dans le cas d'une fonction non régulière, on augmente N jusqu'à ce que l'intégrale
numérique n'évolue pas plus que d'une valeur donnée e.
Cette méthode ne garantit pas d'écart E entre l'intégrale numérique et l'intégrale effective.
Figure
3
: intégration numérique (trapèzes).