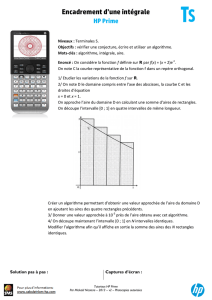
T P fl^ minées. Commentez vos résultats.

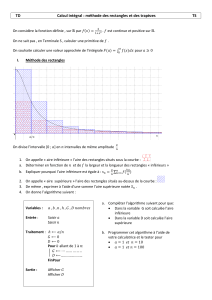
Sujet de TP 3. Intégration numérique
3.21> Calculez la valeur exacte de fl^ f{x)dx et comparez avec les deux valeurs précédemment déter-
minées. Commentez vos résultats.
3.3 > Écrivez en pseudo-code l'algorithme permettant de calculer l'intégrale avec la méthode des
rectangles (pour des rectangles dont le sommet gauche s'appuie sur la courbe). Faites vérifier
l'algorithme par l'enseignant avant de passer à la suite.
3.4 > Écrivez le programme permettant de calculer l'intégrale integr_gauche de la fonction /(x) =
pour des rectangles dont le sommet gauche s'appuie sur la courbe, et integr_droite pour
des rectangles dont le sommet droit s'appuie sur la courbe. L'utilisateur choisira les valeurs de
a, b et n. f sera définie à l'aide d'une fonction que vous placerez au début du programme.
La valeur de l'intégrale sera affichée avec cinq chiffres après la virgule. Vous enregistrerez le
programme dans le dossier TP3 sous le nom rectangles .py.
3.51> En utilisant ce programme, remplissez le tableau 3.1 et commentez-le.
n 1
2 4 50 100 1000
10000
integr_gauche
integr_droite
TABLE 3.1 - Valeur de l'intégrale en fonction de n pour la méthode des rectangles.
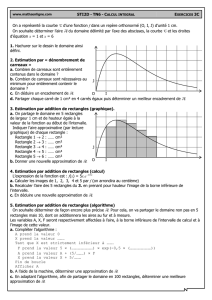
3.1.2 Méthode des trapèzes
Il existe beaucoup d'autres méthodes d'intégration numérique dont l'une, la méthode des tra-
pèzes, est une extension directe de la méthode des rectangles. Elle consiste à remplacer les rectangles
par des trapèzes dont les deux sommets s'appuient sur la courbe de la fonction /.
3.6 > Montrez graphiquement que la surface du trapèze ainsi constitué est la moyenne des surfaces
des rectangles obtenus avec les deux méthodes des rectangles.
3.7 > Déduisez-en que :
f(x)dx « - fia)x
b — a
n
•2f{xi) X
b — a
n +
2/(x„_i) X
b — a
n
f{b) X
3.8 > Écrivez en pseudo-code l'algorithme permettant de calculer l'intégrale de la fonction f{x) —
en utilisant la méthode des trapèzes. L'utilisateur choisira les valeurs de a, betn. f sera définie
à l'aide d'une fonction. Le calcul de l'intégrale sera réalisé par une fonction que vous appellerez
trapèze et qui aura pour paramètres a, b et n. Faites vérifier le pseudo-code par l'enseignant
avant de poursuivre.
3.9 o Écrivez le programme correspondant à l'algorithme de la question précédente. Vous enregistre-
rez le programme sous le nom trapezes.py. La valeur de l'intégrale sera affichée avec cinq
chiffres après la virgule.
3.10 > Optimisez le code de votre programme pour accélérer la vitesse de traitement, à la manière de
ce que vous avez fait pour la méthode des rectangles.
3.111> Vérifiez que la méthode des trapèzes est plus exacte que celle des rectangles pour un même
nombre d'intervalles n. Four cela, vous remplirez le tableau 3.2. Comparez les valeurs avec
celles du tableau 3.1 et commentez.
n
1 2 4 50 100 1000
10000
integr
TABLE 3.2 - Valeur de l'intégrale en fonction de n pour la méthode des trapèzes
18