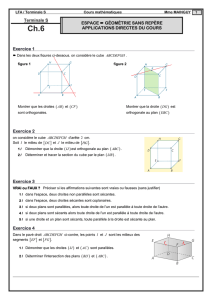
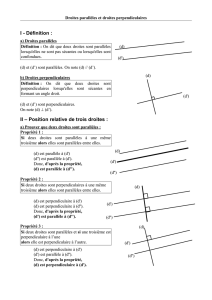
version complétée

•
•
•
d d0Pd
P
dP P
d d0P0P
d0P P0d
PA A d0d d0
dP
P P0Q
P P0

Q P d
P0Q
P0dP P P0
Q P0d0d d0Q
P P0
d d0
P P0dPd0P0
∆P P0
Pd d0
P0P P0
P P0
dP0P P P0
∆d∆d0
∆d d0
P P0
P
P0P P0
d d0∆d
∆0d0∆ ∆0
dP
P

dP
•d A P
• P A d
•d d0Pd
d0
•d d0P
• P P0dP P0
•
•
•∆Pd d0d0
P
•A d0Pd A
Pd0
•∆0P0APdQ
∆0AP∆ ∆0A d
P∆Pd∆ ∆0d
P0dP0
P[AB]I
(AB)
[AB]A B

•~u ~v ~v =k~u k
•A B C −−→ AB −→ AC
•(AB) (CD)−−→ AB −−→ CD
A B
M(AB)x
−−→
AM =x−−→ AB
A B C
M(ABC)x y
−−→
AM =x−−→ AB +y−→ AC
−−→
AB −→ AC M
(ABC)x y −−→ AM =x~u +y~v
x y M −−→ AM =x~u +y~v
R−→ AR =x~u (AB) (ABC)−−→ RM =y~v M
(AC)R(ABC)M
(ABC)

~
i~ j~ k
~u (x;y;z)
~u =x
~
i+y~ j+z~ k
•O A ~u =−→ OA ~ k
~
i~ j∆A~ kP
O~ i~ j S
−→
OS Px y −→ OS =x
~
i+y~ j A
S∆z−→ SA =z~ k
~u =−→ OS +−→ SA =x
~
i+y~ j+z~ k
•~u =x
~
i+y~ j+z~ k=x0
~
i+y0~ j+z0~ k
(x−x0)
~
i+ (y−y0)~ j+ (z−z0)~ k=−→ 0~ i~ j~ k
x=x0y=y0z=z0
•(O;~ i,~ j, ~ k)O
~
i~ j~ k
•~ i=−→ OI ~ j=−→ OJ ~ k=−−→ OK (O;~ i,~ j, ~ k)
(OI) (OJ) (OK)OI =OJ =OK = 1
•x y z ~u =x
~
i+y~ j+z~ k ~u
•M M (O;~ i,~ j, ~ k)
−−→
OM x y z M
~u
x
y
z
~v
x0
y0
z0
(O;~ i,~ j, ~ k)
•~u =~v x =x0y=y0z=z0
•~u +~v
x+x0
y+y0
z+z0