Planche21 optique

TSI2
Physique2
Planche21
Optique
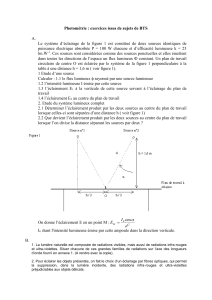
1) La source est monochromatique et de longueur d’onde le milieu assimilé à du vide.
Déterminer l’expression de l’éclairement en un point de l’écran en précisant les
hypothèses et définitions nécessaires.
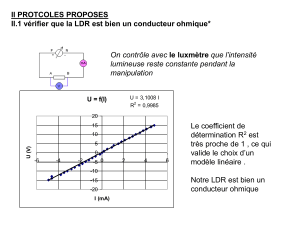
2) La fonction enregistrement (i) du module python représente la figure d’interférence
observée à l’aide les filtres =1,2 et 3 appliqués devant . Donner un encadrement ∆ de la
longueur.
3) Modifier la fonction enregistrement (i) pour déterminer plus précisément en simulant
l’action d’un filtre « plus sélectif »

TSI2
Physique2
Planche21
Corrigé
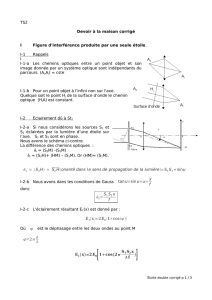
On observe alors, pour ces sources ponctuelles et monochromatiques, une figure d’interférence dont les franges sont
parallèles comme dans le cas de trous d’Young :
Dans ces conditions, nous supposerons que les deux vibrations sont également planes. L’amplitude de la vibration
lumineuse totale est alors donnée par : (,)=(,)+(,)
Avec (,)=cos−
soit ()=
Et : (,)=cos−
soit ()=
A noter que les fentes d’Young sont équivalentes à une superposition de trous d’Young et permettent simplement
d’observer une figure plus lumineuse et plus étendue grâce à la diffraction.
La différence de marche (ou de différence de chemin optique) est donné ici par : =()−()=−
⃗
=′
⃗
+′
⃗
et
⃗
=′
⃗
+′
⃗
Ainsi : =(−
)++
Et : =(+
)++
On trouve alors :−=2
En supposant ≪,≪ et sachant que ≪ :
−≈
donc ≈
L’éclairement ℰ() au point est donné par : ℰ =()×∗()
ℰ =()+()×∗()+∗()
ℰ=
+
+2cos2
=2
(1+∆)
ℰ= 2ℰ(1+∆)
Avec ∆, qui est la différence de phase entre les deux rayons, tel que ∆ =
() et ℰ l’éclairement d’une source prise
isolément.
En appliquant tour à tour les filtres, on en déduit que (600< <750) on obtient ensuite, dans notre cas, =650
1
/
2
100%