TP De la loi binomiale à la loi normale centrée réduite

Académie de Grenoble - Maths et TICE GD
Nom ……………. Prénom ………………. Durée 55 min. Le document comporte deux pages
TP De la loi binomiale à la loi normale centrée réduite
Objectifs : Observer l’évolution de la loi binomiale  selon les valeurs de  et , centrer et réduire pour stabiliser
l’histogramme et maîtriser le comportement global de cette loi. Approximer avec une courbe de Gauss
 Une aide pour Geogebra concernant les mots surlignés se trouve sur une feuille séparée
I-Prérequis (rappels du cours de première)
1. Effet d’une transformation affine sur une variable aléatoire
Soit un entier naturel non nul, et une variable aléatoire ayant pour loi de probabilité :
…
…
L’espérance de  est :  ………….. l’écart-type de  est :  …………………..
Soit et  deux nombres réels. On définit la variable aléatoire  par     
Alors l’espérance de , en fonction de , est :   ……………………
L’écart-type de , en fonction de l’écart-type de  est : ………………………….., donc  …. 
2. Loi binomiale
Si suit la loi binomiale de paramètre  et , alors pour tout compris entre  et  ,
   ……………. ;   …………. et ……………….
Dans toute la suite    et  
II- De la loi binomiale à la loi normale centrée réduite : illustrations avec Geogebra
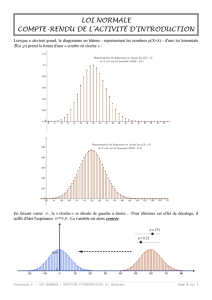
1. Observer la loi binomiale
a. Créer deux curseurs  et   prenant des valeurs entières entre
0 et 100, p prenant des valeurs réelles entre 0 et 1, par pas de
0,01.
Représenter la loi binomiale de paramètres  et . si besoin
recadrer l’affichage
Faire varier les curseurs  et 
b. Au lieu de tracer un diagramme en bâtons, Geogebra trace un
histogramme chaque probabilité élémentaire est donnée par l’aire
d’un rectangle:
- Sur quelles valeurs sont centrées les bases des rectangles
construits par Geogebra ?
…………………………………………………………………………,
- Quelle est la largeur de chaque rectangle ? ……, l’abscisse la plus petite de l’histogramme : …… , la plus grande ………….
- Quelle est l’aire totale de l’histogramme ? ……
Décrire la forme générale de l’histogramme à l’aide d’une courbe connue : ………………………………………………………….
Cette forme reste-t-elle si  est proche de zéro ? Proche de 1 ?
c. Jeu de cible : avec les curseurs, choisir =100 et =0,36. Représenter la fonction définie par   où  et 
désignent deux curseurs,  variant de 0 à 1 par pas de 0.001 et  variant de 0 à 10 par pas de 0.01. Déterminer des valeurs
approchées de  et  telles que la courbe de  représente au mieux l’histogramme.
 …….   …… Comparer une des deux valeurs avec l’écart-type de  : 

Académie de Grenoble - Maths et TICE GD
1/2
2. Centrer la variable aléatoire  suivant la loi binomiale 
a. On définit la variable aléatoire  par      et la variable  par   
 , donc   
Valeurs prises par la variable aléatoire  :  , écart entre deux valeurs successives : …….
Valeurs prises par la variable aléatoire {……………………………………………………… .}, écart entre deux valeurs successives : …….
Valeurs prises par la variable aléatoire  {……………………………………………. ……….. }, écart entre deux valeurs successives : …….
b. « Centrer et réduire » : A l’aide des deux formules encadrées dans les prérequis, sachant  … et  ……………
calculer :   …………. …. et ………………. En modifiant ainsi l’espérance de , on dit que l’on a centré 
  …………. = …. et ……………….. En modifiant ainsi l’écart-type de , on dit que l’on a réduit .
En passant de X à Z, on a centré et réduit X, autrement dit on a effectué une transformation affine pour obtenir une
espérance qui vaut : …….. et un écart type qui vaut ……, ces deux résultats étant indépendants de n et p.
Les lois de ces variables sont représentées dans le fichier Binomiale&NormaleCentreeReduite.ggb
c. Ouvrir ce fichier puis, si besoin, dans Affichage cliquer sur Graphique 2 pour afficher la deuxième fenêtre graphique de
Geogebra. Recadrer l’affichage. Modifier  et  et observer
d. On visualise ainsi trois histogrammes, représentés avec les couleurs violet, orange et bleu :
.Associer à chacun la variable aléatoire qui lui convient : ,  ou  : Violet : ……… Orange : ……… Bleu : ………
Par quelle transformation du plan passe-t-on de l’histogramme en bleu à celui en violet ? …………………………………………………
e. Ces histogrammes représentent des lois de probabilité : l’aire de chaque rectangle représente une probabilité. Donc pour
chaque histogramme, la somme des aires vaut 1
Pour l’histogramme de  la largeur des rectangles est 1, donc la hauteur est   ,  variant de 0 à n.
Pour l’histogramme de  la largeur des rectangles est …. , donc la hauteur est   
Pour l’histogramme de  d’après 2.a., la largeur des rectangles est ………. , donc la hauteur est    
3. Une nouvelle fonction de densité
Un des histogrammes a un aspect qui varie très peu quand on modifie  et  lequel ? ….
Pour le confirmer, afficher la fonction  définie par :
(il suffit de cliquer sur son point). Faire varier  et .
Créer un curseur  variant de -10 à 10 et faire calculer l’intégrale 
 . Quand augmente  se rapproche de …
Facultatif : Etudier la construction des histogrammes

Académie de Grenoble - Maths et TICE GD
2/2
Aide Geogebra
La zone de saisie désigne la ligne à remplir en bas de l’écran
Curseur : pour déplacer précisément un curseur : le sélectionner, puis utiliser les flèches gauche et droite du clavier pour
augmenter ou diminuer la valeur du pas
Loi binomiale (histogramme) : dans la zone de saisie : commencer à taper binomiale, et sélectionner la fonction adéquate
Recadrer le graphique pour adapter rapidement les échelles: cliquer sur le bouton
puis cliquer droit sur le fond et choisir Recadrer
Integrale de f sur [a ;b] : dans la zone de saisie : Integrale(, a, b)