ECN 6578 Module 4 : Temps Continu et des Options

ECN 6578 Module 4 : Temps Continu et des
Options
William McCausland
D´ epartment de Sciences ´ Economiques
Universit´ e de Montr´ eal
13 novembre 2006

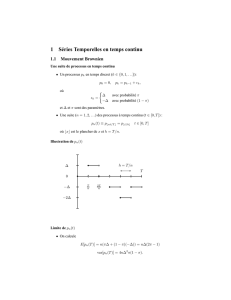
Une suite de processus en temps continu
◮Un processus pken temps discret (k∈ {0,1,...}):
p0=0,pk=pk−1+ǫk,
o`u
ǫk=(∆avec probabilit´
eπ
−∆avec probabilit´ e(1−π)
et ∆et πsont des param` etres.
◮Une suite (n=1,2,...) des processus `
a temps continu
(t∈[0,T]) :
pn(t)≡p⌊nt/T⌋=p⌊t/h⌋t∈[0,T]
o`u ⌊x⌋est le plancher de xet h=T/n.

Illustration de pn(t)
−2∆
−∆
0
∆
T
n2T n
T
h=T/n

Limite de pn(t)
◮On calcule
E[pn(T)] = n(π∆ + (1−π)(−∆)) = n∆(2π−1)
var[pn(T)] = 4n∆2π(1−π).
◮Si on choisit ∆et πen termes de n(ou h) afin que
◮E[pn(T)] = µTpour chaque n
◮var[pn(T)] = σ2Tpour chaque n,
alors
π=1
2 1+µ√h σ!∆ = σ√h.
◮Avec ce choix de π(n)et ∆(n),p(t) = limn→∞ pn(t)est un
MB avec d´ erive µet diffusion σ.

Propri´ et´ es des Mouvements Brownien
◮3 propri´
et´ es de p(t):
1. Pour 0 ≤t1<t2≤T
p(t2)−p(t1)∼N(µ(t2−t1), σ2(t2−t1)).
2. Pour 0 ≤t1<t2≤t3<t4≤T
p(t2)−p(t1)et p(t4)−p(t3)sont ind´ ependants.
3. Tous les chemins ´ echantillonaux (sample paths) sont
continus.
◮Elles peuvent servir de la d´
efinition d’un MB.
◮µ,σet p(0)sp´
ecifie le processus.
◮B(t)est un MB normalis´
e (ou standard): µ=0, σ=1.