Lecon n? 63 - CAPES de Maths

LEÇON N˚ 63 :
Fonction réciproque d’une fonction
strictement monotone sur un intervalle de
R. Étude de la continuité, de la dérivabilité.
Exemples.
Pré-requis :
–Applications injectives, surjectives, bijectives;
–Définitions et propriétés : fonctions monotones, convexes, concaves;
–Notions de continuité, de dérivabilité et de limite;
–Théorème des valeurs intermédiaires.
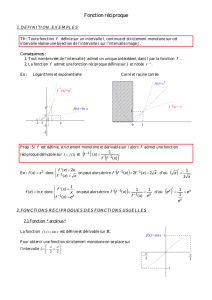
Soit f:I−→ Rune fonction continue et strictement monotone définie sur un intervalle I⊂R.
63.1 Fonctions réciproques
Définition 1 : Soient E, F ⊂R. Une application g:E−→ Fest dite inversible s’il existe une
application h:F−→ Etelle que
h◦g= IdEet g◦h= IdF.
On dit alors que hest la fonction réciproque de get on note h=g−1.
Remarque 1 :
Il faut absolument avoir les deux conditions!!
En effet, dans l’exemple ci-contre, on voit bien que
h◦g= IdE,
mais on a aussi clairement que
g◦h6= IdF.×
×
×
×
×
×
×
×
×
×
×
×
×
×
ghg
h◦gg◦h
E F E F
Proposition 1 : Soient E, F ⊂Ret g:E−→ F.gadmet au plus une fonction réciproque.

2Fonction réciproque; continuité, dérivabilité
démonstration :Soient h1et h2telles que h1◦g=h2◦g= IdEet g◦h1=g◦h2= IdF. Alors
on a h2◦(g◦h1) = h2◦IdF=h2. D’autre part, par associativité, on trouve que h2◦(g◦h1) =
(h2◦g)◦h1= IdE◦h1=h1. D’où h1=h2.
Remarques 2 :
•Cela justifie la notation g−1.
•Si gest inversible, alors g−1l’est aussi et (g−1)−1=g(conséquence de la définition).
Proposition 2 : Soient E, F ⊂Ret g:E−→ F. Alors gest inversible si et seulement si gest
bijective.
démonstration :
"⇒" : Supposons ginversible. Alors pour tous x, x′∈E, on a g(x) = g(x′)⇒g−1g(x)=
g−1g(x′)⇒x=x′d’où l’injectivité de g. Soit alors y∈F. Il s’agit de trouver x∈Etel que
g(x) = y. Or x=g−1(y)convient, d’où la surjectivité de g, et gest finalement bijective.
"⇐" : Supposons gbijective et notons g:x7−→ y. On pose h:F−→ E:y7−→ xet l’on vérifie que
hest aussi bijective, que h◦g= IdEet que g◦h= IdF. On conclut que gest inversible. 
Remarques 3 :
•On vient juste de montrer que si gest inversible, alors g−1est aussi une bijection, de Fdans E.
•Dans un repère normé (dont les vecteurs unitaires sont de même norme), les courbes représentatives de get g−1
sont symétriques par rapport à la droite d’équation y=x.
63.2 Inversibilité de f
Proposition 3 : fest injective si et seulement si fest strictement monotone.
démonstration :
"⇐" : Supposons par exemple fstrictement croissante (l’autre cas se démontrant de manière totale-
ment analogue). Soient x, x′∈I. Alors
f(x) = f(x′)⇔f(x)6f(x′)
f(x)>f(x′)⇔x6x′
x>x′⇔x=x′.
Donc fest injective.
"⇒" : Montrons ce résultat par contraposée et supposons donc fnon monotone. Alors il existe
x1, x2, x3, x4∈Itels que x1< x2⇒f(x1)>f(x2)et x3< x4⇒f(x3)6f(x4). On
pose alors
g(t) = ftx1+ (1 −t)x3−ftx2+ (1 −t)x4.
gest continue sur [0,1] (puisque fl’est par hypothèse sur I) et l’on a g(0) 60et g(1) >0. Le
théorème des valeurs intermédiaires nous permet alors d’en déduire qu’il existe t0∈[0,1] tel que
g(t0) = 0. En posant finalement x5=t0x1+ (1 −t0)x3et x6=t0x2+ (1 −t0)x4, on a x5< x6
et f(x5) = f(x6), c’est-à-dire fn’est pas injective. 

Fonction réciproque; continuité, dérivabilité 3
Remarques 4 :N’oublions pas que toutes ces propriétés sont vraies sous l’hypothèse générale que fest continue
sur un intervalle. Cela nous amène à deux subtilités :
[ ] [ ]
La fonction fdéfinie ci-dessus est injective et continue
(car continue sur chacun des deux intervalles), mais f
n’est pas monotone.
•
Cette fonction est inversible, mais n’est clairement pas
strictement monotone. Le problème vient de la conti-
nuité en 0.
On se gardera donc finalement de dire que les fonctions inversibles sont uniquement les fonctions strictement mono-
tones!
Conséquence : Si f:I−→ f(I)(condition vraie d’après le théorème des valeurs intermédiaires, rajoutant
la surjectivité à la proposition précédente), alors fest bijective (ou inversible selon la proposition 2) si et
seulement si fest strictement monotone.
Dans la suite de la leçon, on notera Jl’intervalle f(I), et f:I−→ f(I) = J.
63.3 Propriétés des fonctions réciproques
Notons avant tout que f:I−→ f(I), supposée être continue et strictement monotone sur l’intervalle I, est
donc inversible, d’inverse notée f−1.
63.3.1 Continuité
Proposition 4 : f−1est strictement monotone sur Jet est de même sens de variations que f. De plus,
f−1est continue sur J.
démonstration :Avant de commencer, nous allons énoncer et démontrer un lemme qui nous sera utile :
Lemme 1 : Soit gune fonction définie sur [a, b], strictement monotone. Si g([a, b]) est un intervalle,
alors gest continue.
démonstration :Supposons gstrictement croissante. Soit c∈[a, b]. On veut montrer que gest
continue en c. Comme gest croissante, les limites à gauche et à droite en cde g(x)existent, valent
respectivement ℓ= sup{g(x), x < c}et L= inf{g(x), x > c}. On a donc ℓ6g(c)6L.
Supposons alors ℓ6=L. Alors x < c ⇒g(x)∈[g(a), ℓ]et x > c ⇒g(x)∈[L, g(b)], donc
]ℓ, L[\{g(c)} 6⊂ [g(a), g(b)] = g([a, b]). Or g([a, b]) est un intervalle, donc celle non inclusion est
impossible, d’où ℓ=L=g(c), donc
lim
x→c
g(x) = g(c).
Si jamais c=aou c=b, on ne regarde que la limite à droite ou à gauche. Finalement, gest continue
en c, donc sur [a, b].2
Nous allons donc pouvoir commencer la démonstration de cette proposition. Supposons fstrictement
croissante. Soient x, x′∈I. Alors x < x′⇒f(x)< f(x′). Posons y=f(x)∈f(I) = Jet

4Fonction réciproque; continuité, dérivabilité
y′=f(x′)∈J. Or f−1(y) = xet f−1(y′) = x′, donc y < y′⇒f−1(y)< f −1(y′)et f−1
est strictement croissante. Pour prouver la continuité de f−1, il suffit alors d’appliquer le lemme avec
g=f−1et [a, b] = f(I). En effet, fcontinue implique que f(I)est un intervalle et f−1f(I)=Iest
un intervalle. 
63.3.2 Dérivabilité
Proposition 5 : Si fest dérivable sur Iet f′ne s’annule pas sur I, alors f−1est dérivable sur J, de
dérivée
(f−1)′=1
f′◦f−1.
démonstration :Soit x0∈Iet ∆ : I\{x0} −→ Rla fonction définie par
∆(x) = f(x)−f(x0)
x−x0
.
On pose y0=f(x0). Pour y∈J\{y0}, on a
f−1(y)−f−1(y0)
y−y0
=f−1(y)−f−1(y0)
f◦f−1(y)−f◦f−1(y0)=f−1(y)−x0
ff−1(y)−f(x0)=1 ∆f−1(y).
Or fest dérivable sur Iimplique que fy est continue, et par la proposition, f−1est continue sur J,
donc f−1(y)−−−→
y→y0
f−1(y0) = x0et ∆(x)−−−→
x→x0
f′(x0)(6= 0 par hypothèse), donc le théorème de
composition des limites nous assure que
lim
y→y0
f−1(y)−f−1(y0)
y−y0
= (f−1)′(y0) = (f−1)′f(x0)=1
f′(x0)=1 f′◦f−1(y0),
ce qui démontre le résultat. 
63.3.3 Autres propriétés
Proposition 6 :
– Si fest impaire, alors f−1est impaire;
– Si fest strictement croissante et convexe (resp. concave), alors f−1est concave (resp. convexe);
– Si fest strictement décroissante et convexe (resp. concave), alors f−1est convexe (resp. concave).
démonstration :
– Pour tout x∈I, on a −f(x) = f(−x). Donc f−1−f(x)=f−1f(−x)=−x. Or on a
aussi f(x) = −f(−x), donc f−1f(x)=x=f−1−f(−x)=f−1f(x). D’où l’égalité
f−1−f(x)=−f−1f(x). En conclusion, pour tout y=f(x)∈f(I), on a f−1(−y) =
−f−1(y).
– Conséquence immédiate de la symétrie entre Cfet Cf−1par rapport à la droite d’équation y=x.
– Conséquence immédiate de la symétrie entre Cfet Cf−1par rapport à la droite d’équation y=x.

Fonction réciproque; continuité, dérivabilité 5
63.4 Exemples
63.4.1 Fonctions ln et exp
Soit fla fonction définie ci-dessous et sa réciproque f−1:
f:R∗
+−→ R
x7−→ ln(x).et f−1:R−→ R∗
+
x7−→ exp(x).
On a alors pour tout x∈R,
(f−1)′(x) = 1
f′◦f−1(x)=1
1
x◦exp(x)
=1
1
exp(x)
= exp(x).
y=x
f−1
f
63.4.2 Fonction racine (n∈N∗)
Soit fla fonction définie ci-dessous et sa réciproque f−1:
f:R+−→ R+
x7−→ xn.et f−1:R+−→ R+
x7−→ x1
n=n
√x.
On a alors pour tout x∈R,
(f−1)′(x) = 1
f′◦f−1(x)=1
nn
√xn−1=1
n xn−1
n
=
n
√x
n x .
y=x
f−1
f
63.4.3 Fonctions trigonométriques
Soit fla fonction définie ci-dessous et sa réciproque f−1:
f: [0, π]−→ [−1,1]
x7−→ cos(x).et f−1: [−1,1] −→ [0, π]
x7−→ arccos(x).
On a alors pour tout x∈R,
(f−1)′(x) = 1
f′◦f−1(x)=1
−sin arccos(x)=−1
√1−x2.
y=x
f−1
f
Remarque :Pour tout x∈[−1,1],sin(arccos x)2+x2= 1 ⇔sin(arccos x) = ±√1−x2. Or sin(arccos 0) =
sin 0 = 1, donc
sin(arccos x) = p1−x2.