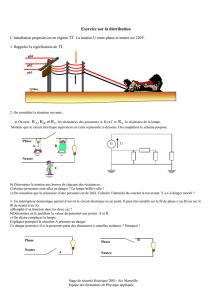
Algèbre Anneaux - Corps

Algèbre
Anneaux - Corps
Denis Vekemans ∗
Solution 3
1. ∀(x, y)∈R2, on pose xLy=x+y−2et xNy=x·y−2x−2y+ 6.
•xLy=x+y−2∈R. Donc Lest une loi interne.
•xL(yLz) = x+y+z−4 = (xLy)Lz. Donc Lest une loi associative.
•xLy=x+y−2 = yLx. Donc Lest une loi commutative.
•xL2 = x. Donc 2est élément neutre pour L.
•xL(4 −x) = 2. Donc tout xest inversible (d’inverse 4−x) par L.
Ainsi, (R,L,2) est un groupe abélien.
2. •xNy=x·y−2x−2y+ 6 ∈R. Donc Nest une loi interne.
•xN(yNz) = x·y·z−2(x·y+y·z+z·x) + 4(x+y+z)−6 = (xNy)Nz. Donc Nest une loi
associative.
•xNy=x·y−2x−2y+ 6 = yNx. Donc Nest une loi commutative.
•xN3 = x. Donc 3est élément neutre pour N.
• ∀x6= 2, x N2x−3
x−2= 3. Donc tout xdifférent du neutre de la loi Lest inversible (d’inverse 2x−3 x−2)
par N.
•xN(yLz) = x·y+x·z−4x−2(y+z) + 10 = (xNy)L(xNz). Donc Nest une loi distributive
par rapport à L.
Ainsi, (R,L,N)est non seulement un anneau commutatif unitaire, mais un corps.
Solution 10 (A, +,·)est un anneau commutatif unitaire intègre et fini. On note 0le neutre de Apour +
et 1le neutre de Apour ·.
Soit φa:x∈A7→ a·x∈Aavec a6= 0.
∗Laboratoire de mathématiques pures et appliquées Joseph Liouville ; 50, rue Ferdinand Buisson BP 699 ; 62 228 Calais
cedex ; France
1

L1 Maths - Info Algèbre 2008
φa(x) = φa(y) =⇒a·x=a·y
=⇒a·(x−y) = 0
=⇒x−y= 0 car Aest intègre et a6= 0
=⇒x=y
Ainsi, φaest injective.
Mais, comme Aest fini, si φaest injective, φaest aussi bijective.
Donc, il existe un unique ytel que a·y= 1 car φaest surjective, donc tout élément non nul de Aest
inversible et Aest un corps.
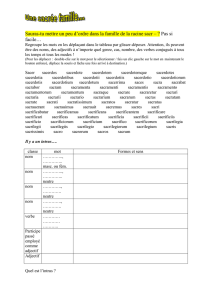
Solution 13 Les endomorphismes du corps Rsont les applications de Rdans Rtelles que
∀(x, y)∈R2, f (x+y) = f(x) + f(y)et f(x·y) = f(x)·f(y).
L’application fidentiquement nulle convient.
De f(0 + 0) = f(0) + f(0), il vient directement que f(0) = 0.
De f(1 ·1) = f(1) ·f(1), il vient directement que f(1) = 0 ou f(1) = 1.
•Premier cas : f(1) = 0.
Alors, ∀x∈R, f(x×1)
|{z }
=f(x)
=f(x)×f(1)
|{z}
=0
= 0 et fest l’application identiquement nulle.
•Deuxième cas : f(1) = 1.
Soit n∈N, on montre aisément par récurrence que f(n) = n(car f(n+ 1) = f(n) + f(1)
|{z}
=1
).
Soit p∈ −N, on a f(p+ (−p))
|{z }
=f(0)=0
=f(p) + f(−p)
|{z }
=−p
puis f(p) = p. Ainsi, ∀p∈Z, f(p) = p.
Soit n∈N∗, on a f(n×1
n)
|{z }
=f(1)=1
=f(n)
|{z}
=n
×f(1
n)puis f(1 n) = 1 n.
Soit p∈Zet n∈N∗, on a f(p
n) = f(p)
|{z}
=p
×f(1
n)
|{z }
=1
n
=p
n. Ainsi, ∀q∈Q, f(q) = q.
On montre maintenant que fest une fonction strictement positive sur R∗
+: si x > 0,f(x) = f(√x)×
f(√x) = (f(√x))2>0.
On en déduit que fest une fonction strictement croissante sur R: si a > b, alors a−b > 0, puis
f(a−b)>0, puis f(a)> f(b)et fest une fonction strictement croissante.
Maintenant on conclut que ∀x∈R, f(x) = xpar un critère de densité (Qest dense dans R) :
∀x∈R,∀ε > 0,∃r1∈Q,∃r2∈Qtels que r1< x < r2et r2−r1< ε, puis par croissance de f,
f(r1)
|{z }
=r1
< f(x)< f (r2)
|{z }
=r2
et f(x)(tout comme x) est dans l’intervalle ]r1, r2[, ce qui conduit à |f(x)−x|< ε,
puis à x=f(x)en faisant tendre εvers 0.
–2/2– Mathématiques