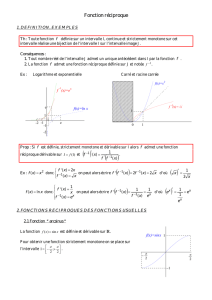
Fonction numérique continue et strictement croissante sur un

Fonction numérique monotone sur un intervalle I de R
Injection
Une fonction strictement monotone sur un intervalle I est injective, c'est à dire que tout élément de f
possède un unique antécédent.
Fonction réciproque
f application de E dans F est inversible s’il existe un, fonction g unique telle que :
g o f = IdE, et f o g = IdF, on note g = f –1 fonction réciproque de f.
Une fonction f est inversible si et seulement si elle est bijective.
Une fonction monotone de I vers f(I) est inversible.
La réciproque est monotone (de même sens de variation que f).
Propriétés relatives à la continuité et aux limites
Points de discontinuité
L'ensemble des points de discontinuité d'une fonction monotone est fini ou dénombrable (on dit qu'il
est au plus dénombrable).
Théorème de la limite monotone pour les fonctions
Soient ]a, b[ un intervalle ouvert (borné ou non) et une fonction croissante f : ]a, b[ R.
Alors :



la fonction admet en tout point x0 une limite à droite et une limite à gauche, qu'on note
respectivement f(x0-) et f(x0+) ; elles vérifient la double inégalité
f(x0-)  f(x0)  f(x0+).
la fonction admet à la borne de droite de l'intervalle une limite, finie ou non ; cette limite est
finie si et seulement si f est majorée, et dans le cas contraire c’est .
la fonction admet à la borne de gauche de l'intervalle une limite, finie ou non ; cette limite est
finie si et seulement si f est minorée, et dans le cas contraire c’est -.
(théorème analogue pour les fonctions décroissantes ; il se déduit immédiatement du
précédent en remplaçant f par -f).
Monotonie et dérivabilité
Soit une fonction f : ]a, b[ R, dérivable sur l'intervalle ]a, b[. Alors :


la fonction f est croissante sur ]a, b[ si et seulement si pour tout x ]a, b[, f’(x)  0.
la fonction f est strictement croissante sur ]a, b[si et seulement si pour tout
x ]a, b[, f’(x)  0. et de plus l'ensemble des points où la dérivée f’ s'annule est d'intérieur
vide (c'est-à-dire que chaque intervalle qu'il contient est vide ou réduit à un point).
(théorème analogue pour caractériser, parmi les fonctions dérivables, celles qui sont
décroissantes, ou strictement décroissantes).
Fonction numérique continue et strictement croissante sur un intervalle I de R
f réalise une bijection de I sur J = f(I) qui est un intervalle.
Soit y0  J (y0 distinct des bornes de J) et x0 = f -1(y0).
Quelque soit  > 0 tel que x1 = x0 -  et x2 = x0 +  soient dan I et = min{f(x0) - f(x1) ; f(x2) - f(x0)}
Pour tout y  ] y0 - , y0 + [, on a f(x1)  y  f(x2).
Par croissance de f –1 on a : x1  f -1(y)  x2 d’où  f -1(y) - f -1(y0)  .
f –1 est continue en y0.
La réciproque d’une fonction monotone continue est continue
Fonction numérique strictement croissante sur un intervalle I de R
Contribution Patrice
J = f(I) n’est pas obligatoirement un intervalle (mais une réunion dénombrable d’intervalles).
Soit y0  J (y0 distinct des bornes de J) et x0 = f -1(y0).
Avec des voisinages :
Quelque soit l’intervalle ]a, b[ contenant x0, aussi petit que l’on veut ] f (a), f (b)[  J est un
voisinage de y0 dont l’image est dans ]a, b[.
f –1 est continue en y0.
La réciproque d’une fonction monotone est continue.
« En coupant les  en quatre… » :
Appliquer le théorème de la limite monotone pour les fonctions : f(x0-)  f(x0)  f(x0+).
Quelque soit  > 0 tel que x1 = x0 -  et x2 = x0 +  soient dan I et = min{f(x0-) - f(x1) ; f(x2) - f(x0+)}
Pour tout y  ] y0 - , y0 + [ J, on a f(x1)  y  f(x2).
Par croissance de f –1 on a : x1  f -1(y)  x2 d’où  f -1(y) - f -1(y0)  .
f –1 est continue en y0.
La réciproque d’une fonction monotone est continue.
Troisième preuve, par l’absurde, en analysant le domaine :
Si f –1 monotone n’était pas continue I serait une réunion dénombrable d’intervalles correspondants
aux points de discontinuité, ce qui est contradictoire avec le fait que I est un intervalle.