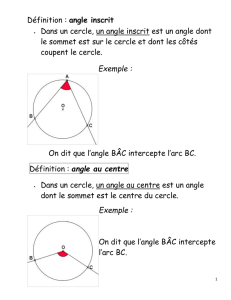
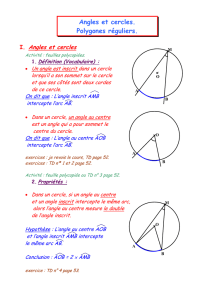
Angles inscrits – Polygones réguliers

Chapitre 13 Angles inscrits – Polygones réguliers 163
Angles inscrits –
Polygones réguliers
EXTRAIT DU B.O. SPÉCIAL N° 6 DU 28 AOÛT 2008
Connaissances Capacités Commentaires
3. Géométrie
3.1 Figures planes
Angle inscrit,
angle au centre
Polygones réguliers
– Connaître et utiliser la relation entre un angle inscrit
et l’angle au centre qui intercepte le même arc.
– Construire un triangle équilatéral, un carré,
un hexagone régulier, un octogone connaissant
son centre et un sommet.
Cette comparaison entre angle inscrit et
angle au centre permet celle de deux angles
inscrits sur un même cercle interceptant le
même arc.
Note : les points du programme (connaissances et capacités) qui ne sont pas exigibles pour le socle commun des connaissances et
des compétences sont en italiques. Certains commentaires ou exemples d’activités, liés à des connaissances et des capacités qui ne
font pas partie du socle, sont écrits en italique dans la troisième colonne mais correspondent à des situations que doivent travailler tous
les élèves car ces connaissances et ces capacités restent des objectifs d’enseignement du programme.
Ouverture
Le cercle de centre O passant par A passe aussi par
les sommets B, C, D, E, F.
On remarque que tous les côtés de l’hexagone
ABCDEF ont la même longueur égale au rayon du
cercle de centre O et tous les angles ont la même
mesure égale à 120°.
Je prends un bon départ
QCM
1
B
2
C
3
A
4
C
5
B
6
B
7
B
8
1. Faux 2. Vrai 3. Vrai 4. Vrai
5. Vrai 6. Faux 7. Vrai
9
• Le triangle ABC est isocèle en A, donc
la hauteur (AH) est également la médiatrice de [BC].
D’où : BH = 1
2 BC = 2 cm.
• Dans le triangle ABH rectangle en H, on a l’égalité
de Pythagore : AB2 = AH2 + BH2,
d’où : AH2 = 72 − 22 = 45
Ainsi : AH = 45 cm, soit : AH ≈ 6,7 cm.
10
a. Dans le triangle AOH rectangle en A, on a :
cos AOH = OA
OH
2
4
1
2
==
= 0,5
Ainsi : AOH = 60°.
b. Le triangle AOB est isocèle en O, donc la médiane
(OH) est également la bissectrice de l’angle AOB .
Ainsi : AOH = 1
2 AOB = 1 2 × 120° = 60°.
c. • Dans le triangle BHO rectangle en H, les angles
HBO et BOH sont complémentaires, donc :
BOH = 90° − 35° = 55°.
• L’angle BOA est droit, donc :
AOH = BOA − BOH = 90° − 55° = 35°.
Activités
1 Objectif
Découvrir le vocabulaire sur les angles au centre et les
arcs de cercle qu’ils interceptent.
1. Les deux points A et B déterminent deux angles
au centre : un angle saillant et un angle rentrant.
2. AOB = 60°. AOB = 360° − 60° = 300°.
3. Les deux points A et B déterminent deux arcs du
cercle Ꮿ : un petit arc et un grand arc.
4. Un seul angle au centre intercepte un arc donné.
5. Un angle au centre qui intercepte un arc plus
grand qu’un demi-cercle est rentrant ; s’il intercepte
un arc plus petit qu’un demi-cercle, il est saillant.
6. L’angle au centre AOD intercepte un demi-cercle si
les points A et D sont diamétralement opposés. Dans
ce cas, l’angle AOD est plat.
2 Objectif
Découvrir le vocabulaire sur les angles inscrits et les arcs
de cercle qu’ils interceptent.
1. a.
Fig. 1 B
S
Ꮿ
A
O
Fig. 2 B
S
ᏯA
O
© Éditions Belin, 2012.

164
c. [CD] étant un diamètre du cercle Ꮿ de centre O :
ACO = ACD.
Le triangle AOC étant isocèle en O, on a :
2 × ACO = 2 × ACD = 180° − AOC.
d. [CD] étant un diamètre du cercle Ꮿ de centre O :
DOC = 180°.
Ainsi : AOD = DOC − AOC = 180° − AOC .
e. D’après les questions c. et d., on a :
2 × ACD = AOD ou : ACD = 1
2 × AOD.
2. a. Sur les deux figures, l’angle inscrit ACB et
l’angle au centre AOB interceptent le même arc AB.
b. • ACD = 1
2 × AOD.
• DCB = 1
2 × DOB.
c. • Sur la figure 1 :
ACB = ACD + DCB = 1
2 × AOD + 1 2 × DOB
= 1
2 × (AOD + DOB) = 1 2 × AOB.
• Sur la figure 2 :
ACB = ACD − DCB = 1
2 × AOD − 1 2 × DOB
= 1
2 × (AOD − DOB) = 1 2 × AOB.
d. Si dans un cercle, un angle inscrit et un angle
au centre interceptent le même arc, alors la mesure
de l’angle inscrit est égale à la moitié de celle de
l’angle au centre.
4 Objectif
Comparer les mesures de deux angles inscrits dans
un cercle interceptant le même arc.
1. a. L’angle au centre AOB intercepte l’arc AB.
b. ACB = 1
2 × AOB et ADB = 1 2 × AOB.
c. D’où : ACB = ADB.
d. Si dans un cercle, deux angles inscrits interceptent
le même arc, alors ils ont la même mesure.
2. Les angles inscrits DGF et DEF interceptent le
même arc DF.
Or, si dans un cercle, deux angles inscrits interceptent
le même arc, alors ils ont la même mesure.
Donc : DGF = DEF = 63°.
5 Objectif
Retrouver, grâce à l’égalité de deux angles inscrits inter-
ceptant le même arc de cercle, le résultat relatif à l’angle
droit vu en 4e.
1. a. COD est l’angle au centre qui intercepte l’arc CD.
b. CAD est un angle inscrit qui intercepte l’arc CD.
2. a. [CD] est un diamètre du cercle Ꮿ de centre O,
donc : COD = 180°.
b. 1re figure :
L’angle inscrit SAB intercepte le petit arc SB.
L’angle inscrit ABS intercepte le grand arc AS.
2e figure :
L’angle inscrit SAB intercepte le petit arc SB.
L’angle inscrit ABS intercepte le petit arc AS.
2. a., b. et c. d.
F
S
T
E
O
F
S
T
E
O
3. Une infinité d’angles inscrits interceptent un arc
donné.
4. Si un angle inscrit intercepte un arc plus grand
qu’un demi-cercle, alors il est obtus.
Si un angle inscrit intercepte un arc plus petit qu’un
demi-cercle, alors il est aigu.
Si un angle inscrit intercepte un arc égal à un demi-
cercle, alors il est droit (voir démonstration activité 5).
3 Objectifs
– Conjecturer la relation entre la mesure d’un angle
inscrit et celle de l’angle au centre qui intercepte le
même arc à l’aide d’un logiciel de géométrie.
– Démontrer cette conjecture.
A. 1. a., b., c., d. et e.
f. On constate que la mesure de l’angle inscrit ACB
est égale à la moitié de celle de l’angle au centre AOB.
2. a. Si l’on déplace le point C sur le cercle, on constate
également que la mesure de l’angle inscrit ACB est
égale à la moitié de celle de l’angle au centre AOB.
b. Si l’on déplace les points A et B sur le cercle, on
fait encore la même constatation.
B. 1. a. L’angle inscrit ACD et l’angle au centre AOD
interceptent le même arc AD.
b. A et C étant deux points du cercle Ꮿ de centre O,
on a : OA = OC. Par conséquent, le triangle AOC est
isocèle en O.
© Éditions Belin, 2012.

Chapitre 13 Angles inscrits – Polygones réguliers 165
b. L’angle inscrit CAD et l’angle au centre COD l’angle
au centre interceptent le même arc vert CD, donc :
CAD =1
2× COD = 1 2× 180° = 90°.
3. On retrouve la propriété vue en 4e :
Si un triangle est inscrit dans un cercle ayant pour
diamètre l’un de ses côtés, alors ce triangle est
rectangle et son hypoténuse est ce côté.
4. a. L’angle inscrit CED intercepte l’arc CD.
D’où : CED = 1
2 × COD = 1 2 × 180° = 90°.
Le triangle CED est donc rectangle en E.
b. Si le triangle CFD est rectangle en F, alors le point
F est situé sur le cercle Ꮿ.
L’angle CFD intercepte le demi-cercle CD.
6 Objectif
Connaître la défi nition d’un polygone régulier.
Les polygones réguliers sont les figures :
• b. En effet, un triangle équilatéral a ses trois côtés de
même longueur et ses trois angles de même mesure.
• e. En effet, un carré a ses quatre côtés de même
longueur et ses quatre angles de même mesure.
7 Objectifs
– Déterminer la mesure de chacun des « angles au centre »
d’un polygone régulier.
– Construire un triangle équilatéral, un carré
SC3
, un
hexagone régulier, un octogone régulier connaissant son
centre et un sommet.
1. a.
BC
A
O
b. •Le triangle ABC est équilatéral, donc :
BAC = ABC = ACB = 60°.
• L’angle inscrit ACB et l’angle au centre AOB
interceptent le même arc AB, donc : ACB = 1
2 × AOB.
Ainsi : AOB = 2 × ACB = 2 × 60° = 120°.
On démontre de la même façon que :
BOC = 2 × BAC = 120° et COA = 2 × ABC = 120°.
c. E
D
F
I
120°
Ꮿ
2. a. ABCD est un carré donc ses diagonales sont
perpendiculaires, ainsi :
AOB = BOC = COD = DOA = 90°.
b. S
I
U
3 cm RT
3. a. 360
6
° = 60°, ainsi :
AOB = BOC = COD = DOE = EOF = FOA = 60°.
A
B
D
EF
C
60°
Ꮿ
O
b. Chacun des 6 triangles est isocèle en O et a un
angle mesurant 60°, donc il est équilatéral.
c. AOB étant un triangle équilatéral, on a :
AB = OA = OB.
En procédant de la même façon avec les 5 autres
triangles équilatéraux, on montre que tous les côtés
de l’hexagone ABCDEF ont une même longueur
égale au rayon du cercle de centre O.
d. D’après la question b :
OBA = OBC = 60°, ainsi :
ABC = OBA + OBC = 60° + 60° = 120°.
On démontre de la même façon que :
BCD = CDE = DEF = EFA = FAB = 120°.
e. L’hexagone ABCDEF a tous ses angles de même
mesure et tous ses côtés de même longueur, c’est
donc un hexagone régulier.
f.
A
B
D
E
F
C
60°
Ꮿ
O
4. a., b. et c. 360
8
° = 45°
• On place un point B sur le cercle tel que :
AOB = 45°.
• On place sur ce cercle les points distincts C, D, E, F,
G et H tels que : AB = BC = CD = DE = EF = FG = GH.
• On trace les cordes [AB], [BC], [CD], [DE], [EF],
[FG], [GH] et [HA], et on obtient l’octogone régulier
ABCDEFGH inscrit dans le cercle de centre O.
© Éditions Belin, 2012.

166
Savoir-faire
11
1. a. 30° b. 43° c. 55°
d. 90° e. 120° f. 155°
2. a. 240° b. 50° c. 280°
d. 180° e. 90° f. 200°
12
1. L’angle inscrit EFG et l’angle au centre EOG
interceptent le même arc de cercle EG.
Or, si dans un cercle, un angle inscrit et un angle au
centre interceptent le même arc, alors la mesure de
l’angle inscrit est égale à la moitié de celle de l’angle
au centre.
Donc : EOG = 2 × EFG = 2 × 55° = 110°.
2. Les angles inscrits GFI et IHG interceptent le même
arc de cercle IG.
Or, si dans un cercle, deux angles inscrits interceptent
le même arc, alors ils ont la même mesure.
Donc : GFI = IHG = 40°.
13
SC3
AOB = BOC = COD = DOE = EOF = FOA
= 360
6
° = 60°
A
B
D
EF
C
60°
60°
60°
60° 60°
60°
O
14
AOB = 360
5
° = 72°
A
B
D
E
C
72°
72°
72° 72°
4 cm
72°
O
15
3 cm
16
1.
O
A
P
x
By
Ꮿ
2. Il semble que la demi-droite d’origine O passant
par P est toujours la même quelle que soit la position
prise par le demi-cercle Ꮿ avec A sur [Ox) et B sur
[Oy).
Exercices
À l’oral
17
L’angle inscrit et l’angle au centre interceptent
le même arc sur les figures a, b et e mais pas sur les
figures c, d et f.
18
a. SPR et SOR interceptent l’arc RS.
b. SPT et SOT interceptent l’arc TS.
c. RSP et ROP interceptent l’arc RP.
d. STP et SOP interceptent l’arc SP.
19
Angle inscrit Angle au centre
EIH •
IFH •
FHI •
EHF •
EHI •
• IOH
• EOI
• EOH
• IOF
• EOF
20
1. a. 72° b. 156° c. 180° d. 242°
2. a. 18° b. 40° c. 45° d. 70°
21
Les polygones réguliers correspondent aux
figures c et d.
22
1. • Penta : 5 • Hepta : 7
• Deca : 10 • Hexa : 6
• Ennea : 9 • Hendeca : 11
• Octo : 8 • Dodeca : 12
2. • Polygone à 5 côtés : pentagone
• Polygone à 6 côtés : hexagone
• Polygone à 7 côtés : heptagone
• Polygone à 8 côtés : octogone
• Polygone à 9 côtés : ennéagone
• Polygone à 10 côtés : décagone
• Polygone à 11 côtés : hendécagone
• Polygone à 12 côtés : dodécagone
23
1. Vrai 2. Vrai 3. Vrai
4. Faux. En effet, le symétrique du triangle ACD par
rapport à O est le triangle AOF.
5. Vrai 6. Vrai 7. Vrai 8. Vrai 9. Vrai.
© Éditions Belin, 2012.

Chapitre 13 Angles inscrits – Polygones réguliers 167
• SOD = COD − COS = 180° − 100° = 80°.
• DRS = 1
2 × SOD = 1 2 × 80° = 40°.
29
• Les angles inscrits HIP et RSP interceptent le
même arc HR.
Or, si dans un cercle, deux angles inscrits interceptent
le même arc, alors ils ont la même mesure.
Donc : HIP = RSP = 30°.
• HPI = 180° − (70° + 30°) = 180° − 100° = 80°.
30
• L’angle inscrit DFE et l’angle au centre DOE
interceptent le même arc de cercle DE.
Or, si dans un cercle, un angle inscrit et un angle au
centre interceptent le même arc, alors la mesure de
l’angle inscrit est égale à la moitié de celle de l’angle
au centre.
Donc : DOE = 2 × DFE = 2 × 30° = 60°.
• D et E étant deux points du cercle Ꮿ de centre O,
on a : OD = OE. Le triangle ODE est donc isocèle en O.
• ODE est isocèle en O et DOE = 60°.
Or, un triangle isocèle ayant un angle de 60° est
équilatéral, donc le triangle ODE est équilatéral.
31
• Les angles inscrits EAB et EFB interceptent le
même arc EB.
Or, si dans un cercle, deux angles inscrits interceptent
le même arc, alors ils ont la même mesure.
Donc : EAB = EFB = 70°.
•Le triangle AEB est inscrit dans le cercle Ꮿ de
diamètre [AB], donc le triangle AEB est rectangle en E.
Ainsi : AEB = 90°.
• ABE = 180° − (90° + 70°) = 180° − 160° = 20°.
32
1. L’angle inscrit ULI et l’angle au centre UOI
interceptent le même arc de cercle UI.
Or, si dans un cercle, un angle inscrit et un angle au
centre interceptent le même arc, alors la mesure de
l’angle inscrit est égale à la moitié de celle de l’angle
au centre.
Donc : UOI = 2 × ULI. D’où : x + 45° = 2 × 2x = 4x.
Soit : 3x = 45°, d’où : x = 45
3
° = 15°.
2. • UOI = 15° + 45° = 60°.
• Le triangle OUI est isocèle en O et UOI = 60°, donc
OUI est un triangle équilatéral.
33
1. • Les angles inscrits JRS et JIS interceptent
le même arc JS.
Or, si dans un cercle, deux angles inscrits interceptent
le même arc, alors ils ont la même mesure.
Donc : JRS = JIS = 25°.
• L’angle inscrit RSJ et l’angle au centre ROJ
interceptent le même arc de cercle RJ.
Or, si dans un cercle, un angle inscrit et un angle au
centre interceptent le même arc, alors la mesure de
l’angle inscrit est égale à la moitié de celle de l’angle
au centre.
Donc : RSJ = 1
2 × ROJ = 1 2 × 90° = 45°.
• RJS = 180° − (25° + 45°) = 180° − 70° = 110°.
Je m’entraîne
24
a. L’angle inscrit ACB et l’angle au centre AOB
interceptent le même arc de cercle AB.
Or, si dans un cercle, un angle inscrit et un angle au
centre interceptent le même arc, alors la mesure de
l’angle inscrit est égale à la moitié de celle de l’angle
au centre.
Donc : ACB = 1
2 × AOB = 1 2 × 76° = 38°.
b. De même : ACB = 1
2 × AOB = 1 2 × 220° = 110°.
25
L’angle inscrit IJK et l’angle au centre IOK
interceptent le même arc de cercle IK.
Or, si dans un cercle, un angle inscrit et un angle au
centre interceptent le même arc, alors la mesure de
l’angle inscrit est égale à la moitié de celle de l’angle
au centre.
Donc : • IOK = 2 × IJK = 2 × 65° = 130°.
• De même : JIK = 1
2 × JOK = 1 2 × 110° = 55°.
26
1. a. et b.
K
J
I
O
5 cm
75°
50°
2. • Dans le triangle IJK :
IKJ = 180° − (75° + 50°) = 180° − 125° = 55°.
• L’angle inscrit IKJ et l’angle au centre IOJ
interceptent le même arc de cercle IJ.
Or, si dans un cercle, un angle inscrit et un angle au
centre interceptent le même arc, alors la mesure de
l’angle inscrit est égale à la moitié de celle de l’angle
au centre.
Donc : IOJ = 2 × IKJ = 2 × 55° = 110°.
27
Les angles inscrits DNB et BID interceptent le
même arc BD.
Or, si dans un cercle, deux angles inscrits interceptent
le même arc, alors ils ont la même mesure.
Donc : DNB = BID = 41°.
28
• L’angle inscrit CDS et l’angle au centre COS
interceptent le même arc de cercle CS.
Or, si dans un cercle, un angle inscrit et un angle au
centre interceptent le même arc, alors la mesure de
l’angle inscrit est égale à la moitié de celle de l’angle
au centre.
Donc : CDS = 1
2 × COS = 1 2 × 100° = 50°.
© Éditions Belin, 2012.