Page 1 FONCTION LOGARITHME NEPERIEN : f(x) = ln(x) I

FONCTION LOGARITHME NEPERIEN : f (x) = ln(x)
I) DEFINITION.
a) Définition 1 et notations : ( de la fonction logarithme )
La fonction logarithme népérien notée « ln », associe à tout nombre réel x positif strict le nombre
réel noté ln(x) ou ln x et appelé le logarithme népérien de x. On note : ln : ] 0 , + ∞ [
→
IR
x
→
ln(x)
C’est l’unique fonction telle que :
(1) la dérivée de la fonction logarithme népérien est la fonction inverse : x
→
1
x .
(2) La valeur du logarithme népérien de 1 vaut 0.
Avec les notations ci dessus on a par définition : [ln(x)]’ = 1
x
ln(1) = 0
(admis )
• Remarque : la valeur de ln(x) est donné par une table de logarithmes ou par une calculatrice.
Par exemple la calculatrice donne : ln(2) ≈ 0,693 à 10
–3
près ; ln( 1
2 ) = – 0,693 à 10
–3
près.
II) PROPRIETES GENERALES .
A) Propriété 1 : ( Domaine de définition ) :
La fonction logarithme népérien f(x) = ln x est définie pour x ∈ ]0 ; + ∞ [.
Seuls les nombres réels positifs stricts admettent un logarithme népérien.
Soit a un nombre réel, ln(a) n’existe que si a > 0.
( 0 , –1 , –3 , … n’ont pas de logarithme népérien )
Application :
 Soit f la fonction définie par f(x) = ln( x – 3).
ln(x – 3) n’existe que si x – 3 > 0 donc si x > 3 , le domaine de définition de f est D
f
= ] 3 ; + ∞[.
B) Propriétés de base :
Propriété 2 :
Quels que soient les nombres réels a et b positifs stricts
ln(ab) = ln(a) + ln (b) ( ln « transforme » les multiplications en additions )
Exemples :
 ln(6) = ln(2×3) = ln2 + ln3  ln5 + ln2 = ln(5×2) = ln10  ln1 +ln 1 = ln(1×1) = ln1 = 0.
Propriété 3 :
Quel que soit les nombres réels positif strict a et b
ln (a
b
) = b×ln(a) ( ln « transforme » les puissances en multiplications )
Exemples :
 ln(6²) = 2ln(6)  ln(x²) = 2ln(x)  ln(x
3
) = 3 ln(x)  ln( x) = ln (x
1/2
) = 1
2 ln(x) ;
 ln( 1
x ) = ln(x
– 1
) = –1×ln(x) = – ln(x).

Remarque :
On a en particulier : ln(x²) = 2ln(x) ; ln(x
3
) = 3ln(x) ; ln( x) = 1
2 ln(x) ; ln( 1 x ) = –ln(x).
Propriété 4 :
Quel que soit les nombres réels positif strict a et b :
ln ( a
b ) = ln(a) – ln(b) ( ln « transforme » les divisions en soustraction )
Exemples :  ln( 2
3 ) = ln(2) – ln (3)  ln (5) – ln( 7) = ln ( 5 7 ).
III) DERIVEE :
a) Propriété 5 : ( dérivée de lnx et de ln u(x) )
(1) La fonction ln est dérivable sur ]0 ; + ∞ [ et sa dérivée est la fonction inverse : [ln(x)]’ = 1
x
(2) Si u est une fonction dérivable, positive strict sur I ⊂ IR alors [ln u(x)]’ = u’(x)
u(x)
b) Exemples :
 Si f(x) = 3x² + 4x – 1 + ln x pour x ∈ ]0 ; + ∞ [ alors f ’(x) = 6x + 4 + 1
x .
 Si f(x) = ln(x² + 2) sur IR alors f(x) = ln u(x) où u(x) = 3x² + 2 donc u’(x) = 6x
u(x) = 3x² + 2 est positif pour tout x ∈ IR
donc f ’(x) = u’(x)
u(x) = 6x 3x² +2 .
IV) SENS DE VARIATION :
Propriété 6 : ( variations de la fonction logarithme )
La fonction ln croît strictement sur ] 0 ;+ ∞ [ car sa dérivée x
→
1
x est positive pour x > 0.
Valeurs de x 0 + ∞
Signe de ln’(x) = 1
x
+
Variations de ln + ∞
– ∞ ( limites vu au V) )
V) LIMITES :
a) Propriété 7 : ( limites de ln(x) en + ∞ en 0
+
et en a > 0 )
• La limite de ln(x) en + ∞ est + ∞ : lim
x → + ∞
ln(x) = + ∞ un logarithme est aussi grand qu’on veut
• La limite de ln(x) en 0
+
est – ∞ : lim
x → 0
x > 0
ln(x) = – ∞ . un logarithme est aussi petit qu’on veut.
donc la droite d’équation x = 0 est asymptote verticale à la courbe de ln .
Remarque : Sur ]0 ; + ∞ [ , la fonction logarithme n’admet ni maximum, ni minimum.

Propriété 8 :
• Si a > 0 alors la limite de ln(x) quand x tend vers a est ln(a) : lim
x →a
ln(x) = ln(a)
b) Propriété 9 : ( croissances comparées ).
• ln(x) croît moins vite que n’importe quelle puissance positive de x , c’est à dire :
Quel que soit n ∈ IN-{0} on a : lim
x → + ∞
ln(x)
x
n
= 0 en particulier lim
x → + ∞
ln(x)
x = 0
• Quel que soit n ∈ IN-{0} lim
x → 0
x > 0
x
n
ln(x) = 0 en particulier lim
x → 0
x > 0
xln(x) = 0 .
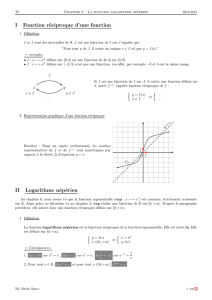
VI) TABLEAU de VALEURS et COURBE REPRESENTATIVE :
x 0,05
0,1 0,25 0,5 1 2 3 4 5 10 15 20 25 100 1000000
ln(x)
≈ –3 ≈ –2,3 ≈ –1,4 ≈ –0,69
0
≈ 0,7 ≈ 1 ≈ 1,4 ≈ 1,6 ≈ 2,3 ≈ 2,7 ≈ 3 ≈ 3,2 ≈ 4,6 ≈ 13,8
VII) EQUATIONS :
a) Propriété 10 : ( égalité de logarithmes )
•Quels que soient les réels a > 0 et b > 0 ln(a) = ln(b) équivaut à a = b .
Exemples :
 On cherche à résoudre l’équation : ln(2x) = ln ( x + 1)
a) on précise le domaine de définition de l’équation: ln 2x n’existe que si x > 0 et ln(x+1) si x > –1
donc l’équation n’a de sens que si x ∈ ] 0 ; + ∞ [ on écrit : D = ]0 ; + ∞
∞∞
∞ [ .
b) on résout l’équation :
ln(2x) = ln ( x + 1) donc 2x = x +1 donc x = 1
c) on vérifie que la ( ou les ) solution trouvée est bien dans D et on conclue : 1 ∈ D donc : S = {1}.
x
y
0123456789
-6
-4
-2
0
2
L’axe (oy) est asymptote verticale

 On cherche à résoudre l’équation : ln(3x) = ln ( 2x – 1) .
a) l’équation n’a de sens que si x > 0 et x > 1
2 donc D = ] 1 2 ; + ∞ [ .
b) ln(3x) = ln ( 2x – 1) donc 3x = 2x –1 donc x = –1
c) –1 ∉ D = ] 1
2 ; + ∞ [ donc S = ∅.
b) Propriété 11 : ( antécédents de nombres par la fonction logarithme ).
• Il existe un unique nombre noté « e » ( 2,718 < e < 2,719) tel que ln(e) = 1 .
Autrement dit : ln(x) = 1 ⇔ x = e ≈ 2,718.
Le nombre « e » est appelé la base des logarithmes népériens.
• Quel que soit le nombre a ∈ IR on a : ln(x) = a ⇔ x = e
a
( exponentiel de a )
Exemples
 Si ln(x) = 2 alors x = e
2
≈ 7,4 et S = {e²}
 Si ln(x) = –2 alors x = e
–2
≈ 0,13 et S = { e
–2
}
VII) INEQUATIONS :
a) Propriété 12 : ( inégalité de logarithmes ) .
•Quels que soient les réels a > 0 et b > 0 : ln(a) > ln(b) ⇔ a > b . ( idem pour <, ≤ , ≥ )
Exemple :
 On cherche à résoudre l’inéquation : ln(2x) > ln ( 2 – x) .
a) Le domaine de définition de l’inéquation est D = ] 0 ; 2 [
b) ln(2x) > ln ( 2 – x) donc 2x > 2 – x donc 3x > 2 donc x > 2
3 .
c) Or D = ] 0 ; 2 [ donc S = ] 2
3 ; 2 [.
b) Propriété 13 : ( antécédents de nombres par la fonction logarithme ).
• Quel que soit le nombre a ∈ IR et x > 0 ln(x) > a ⇔ x > e
a
( idem pour <, ≤ , ≥ )
Exemples :
 Si ln(x) > 2 alors x > e
2
≈ 7,4 et S = [e² ; + ∞[
 Si ln(x) < –2 alors x < e
–2
≈ 0,13 S = ] 0 ; e
–2
[
c) Propriété 14 : ( signe de ln(x) )
ln(x) est négatif pour 0 < x < 1
ln(x) est positif pour x > 1
ln(x) est nul pour x = 1
.
Valeur de x 0 1 +
∞
Signe de ln(x) – 0 +

TEST : FONCTION LOGARITHME NEPERIEN Nom :
………..…………..…………..…………..…
•
••
•Exercice 1 :
a) Quelle est la fonction vérifiant les deux conditions suivantes ? et comment la note t-on ?
(1) elle a pour dérivée f(x) = 1
x
(2) elle vaut 0 si x = 1.
b) Donner les valeurs suivantes à 10
–3
près : ln 2 ≈
………..…………..…
ln 4
3 =
………..…………..…
c) Le nombre ln x existe t-il pour toutes les valeurs de x ∈ IR ? si non, pour quelles valeurs de
x ∈ IR existe t-il ?
d) Donner la valeur de ln(-2) à 10
–3
près si possible : ln(-2) ≈
………..…………..…
•
••
• Exercice 2 :
a) Démontrer que pour tout x > 0 on a : ln ( 3x
3
+ 2x² ) = 2ln x + ln (3x + 2).
b) Démontrer que pour tout x > 0 on a : ln ( x
3
x + 1 ) = 3ln x – ln (x + 1).
•
••
• Exercice 3 :
a) Donner la dérivée de la fonction suivante :
f(x) = 3x² + 4x – 1 + ln x pour x ∈ ]0 ; + ∞ [
b) Donner la dérivée de la fonction suivante :
f(x) = ln(x² + 2) sur IR
•
••
• Exercice 4 : Compléter le tableau de variations de la fonction f(x) = ln(x)
Valeurs de x
Signe de f ’(x)
Variations de ln
•
••
• Exercice 5 :
1)Compléter a) lim
x → + ∞
ln(x) =
………..…
b) lim
x → 0
x > 0
ln(x) =
………..…
c) Si a > 0 , lim
x →a
ln(x) =
………..…
d) lim
x → + ∞
ln(x)
x =
………..…
e) Pour n ∈ IN-{0} , lim
x → + ∞
ln(x)
x
n
=
………..…
e) lim
x → 0
x > 0
xln(x) =
………..…
f) Pour n ∈ IN-{0} , lim
x → 0
x > 0
x
n
ln(x) =
………..…