Intégrale

Chapter 1 Primitives et Intégrales
1

Part I
Primitives
2

Part II
Intégration
3

1.1 Notion d’intégrale d’une fonction
Le plan étant muni d’un repère orthogonal O; ! i ; ! j, on dé…nit les points I,Jet Kpar ! OI =! i ; ! OJ =! j
, = et OIKJ est un rectangle. L’aire du rectangle OIKJ dé…nit alors l’unité d’aire (u.a.).
1.1.1 Aire et intégrale d’une fonction positive
1.1.1.1 Dé…nition
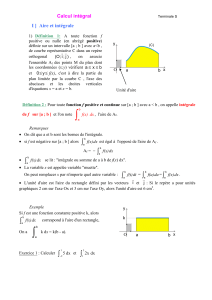
Soit f une fonction continue et positive sur un intervalle [a;b]et Csa courbe représentative dans le repère
O; !
i ; ! j:L’intégrale de aàbde fest le réel noté Zb
a
f(x)dx , égal à l’aire, exprimée en unités d’aire, du
domaine Ddélimité par C, l’axe des abscisses et les droites d’équations x=aet x=b.
Remarque aet bsont les bornes de l’intégrale et xest une variable muette : elle n’intervient pas dans le
résultat. On peut la remplacer par les lettres tou u, ainsi : Zb
a
f(x)dx =Zb
a
f(t)dt =Zb
a
f(u)du:
Exemples : a) Z0
2
3dx = 6:b) Z3
1
xdx =2(3+1)
2= 4:
1.1.2 Valeur moyenne
1.1.2.1 Dé…nition
Soit fune fonction continue et positive sur un intervalle [a;b]avec a < b. La valeur moyenne de fsur [a;b]
est le réel =1
baZb
a
f(x)dx:
Remarque : =1
baZb
a
f(x)dx () (ba) = Zb
a
f(x)dx:
Donc la valeur moyenne de fsur [a;b]est donc le réel tel que le rectangle de dimensions et basoit de
même aire que le domaine Ddélimité par la courbe représentant f, l’axe des abscisses et les droites d’équations
x=aet x=b:
4

1.2 Intégrale et primitive
1.2.1 Intégrale d’une fonction continue, positive et croissante sur un intervalle [a;b]
1.2.1.1 Théorème
Soit fune fonction continue, positive et croissante sur un intervalle I= [a;b]. On note C, sa courbe
représentative dans le plan muni d’un repère orthogonal.
On dé…nit sur [a;b]la fonction A:x7! Zx
a
f(t)dt et on …xe xodans [a;b].
Cette fonction Aest dérivable sur Iet sa dérivée est f:
Preuve
On …xe xodans [a;b]:L’aire de la surface coloriée est A(xo):(…gure 4).
On a hf(xo)A(xo+h)A(xo)hf(xo+h), puisque fest croissante sur I:
Selon que h >0 ou h <0 , on a :
f(xo)A(xo+h)A(xo)
hf(xo+h)ou f(xo+h)A(xo+h)A(xo) hf(xo):
Comme fest continue sur I, donc lim
h!0f(xo+h) = f(xo), et d’après le théorème des gendarmes, il en résulte
lim
h!0
A(xo+h)A(xo)
h=f(xo):
Donc Aest dérivable en a et A0(xo) = f(xo);pour tout xo2I.
1.2.2 Primitive d’une fonction continue
1.2.2.1 Théorème admis
Soit fune fonction continue sur un intervalle [a;b]:Alors la fonction dé…nie sur [a ; b] par (x) = Zx
a
f(t)dt
est l’unique primitive de fsur [a;b]qui s’annule en a:
Remarques
La fonction , dé…nie dans le théorème, est donc dérivable sur [a;b], de dérivée f:
Ce résultat montre que toute fonction continue sur [a;b]admet une, donc des primitives sur [a;b]:
Plus généralement, toute fonction continue sur un intervalle Iquelconque admet des primitives.
Soit Fune primitive quelconque de fsur [a;b], alors Zb
a
f(t)dt =F(b)F(a):
En e¤et, il existe une constante ktelle que pour tout xde [a;b],F(x) = (x) + k. Alors :
F(b)F(a) = (b) + k(a)k= (b)(a) = (b) = Zb
a
f(t)dt puisque (a) = 0.
1.2.3 Généralisation de l’intégrale à l’aide d’une primitive
1.2.3.1 Propriété et dé…nition
Soit fune fonction continue sur un intervalle Iet Fune primitive quelconque de fsur I. Pour tous réels a
et bde I, la di¤érence F(b)F(a)ne dépend pas de la primitive de fchoisie.
On dé…nit alors l’intégrale de aàbde fpar Zb
a
f(t)dt =F(b)F(a):
On écrit aussi : Zb
a
f(t)dt = [F(x)]b
a=F(b)F(a):
Exemple
Z1
2
(xx3)dx =hx2
2x4 4i1
2=12
214 4(2)2 2(2)4 4:=::: =9 4:
1.3 Propriétés de l’intégrale
1.3.1 1ère propriété
Za
a
f(t)dt = 0
5