TS-Cours P02 Mécanique classique

TS www.pichegru.net 19 décembre 2016
-1-
P2 : Mécanique classique
Plan du chapitre
Rappels de math
Dérivées & primitive d’une fonction
Vecteurs
Cinématique
Préalables
Grandeurs étudiées
Différents types de mouvement
Les forces à connaître
Force d’attraction gravitationnelle
Force de réaction d’un support
Force de frottement
Poussée d’archimède
Force électrique
Les 3 lois de Newton
Référentiel galiléen
n°1 : Principe d’inertie
n°2 : Relation fondamentale de la dynamique (RFD)
n°3 : Principe des actions réciproques
Quantité de mouvement
Définition
Conservation de la quantité de mouvement
Système ouvert
Mouvements dans un champ uniforme
Types de mouvement
Forces et champs
Équations du mouvement
Orbites
Mouvement général : l’ellipse
Lois de Kepler
Cas particulier : Mouvement circulaire
Énergie mécanique
Énergie cinétique
Énergies potentielles
Énergie mécanique
Travail d’une force
Définition
Forces conservatives
Forces de frottement
Conservation de l’énergie mécanique
R
R
Ra
a
ap
p
pp
p
pe
e
el
l
ls
s
s d
d
de
e
e m
m
ma
a
at
t
th
h
h
D Dé ér ri iv vé ée es s & & p pr ri im mi it ti iv ve e d d’ ’u un ne e f fo on nc ct ti io on n
Dérivée d’une fonction
En math, la dérivée de f (x) est notée f’(x) :
En physique, la dérivée de f (x) est notée
x
xf
d
)(d ou, plus simplement x f
d
d
Cette notation est beaucoup plus rigoureuse car :
- On sait par rapport à quelle variable on dérive (le plus souvent selon le
temps t, en physique)
- La dérivée est le rapport de la variation infinitésimal de f(x), noté df ,
lorsque la variation ∆ x → 0, cette variation étant notée dx . Cette notation
en rend bien compte.
x
f
d
den physique = f’(x) en math
Remarque : en physique, toutes les fonctions sont dérivables une infinité
de fois, jusqu’à preuve du contraire. Il est donc inutile de savoir si on peut
dériver une fonction avant de calculer sa dérivée. Comme disent les
physiciens : « on dérive, et puis si ça ne marche pas, c’est qu’on n’avait
pas le droit de dériver... ».
Dérivée seconde
La dérivée seconde d’une fonction est la dérivée de sa dérivée. C’est-à-
dire :
x
f
xd
d
d
ddont la notation devient :
2
2
d
d
x
f
Exercice 1 Dérivée d’une fonction
Primitive d’une fonction
Une primitive g(t) d’une fonction f(t) est telle que :
)(
d
dtf
t
g=
Il en existe une infinité, car si g(t) est une primitive de f(t), alors g(t) + k,
avec k un réel, l’est aussi.
La connaissance de la valeur de g à un certain temps t est nécessaire si l’on
veut complètement connaître l’expression complète de g.
Exercice 2 Primitive d’une fonction
V Ve ec ct te eu ur rs s
Un vecteur est défini par ses coordonnées (généralement 3 en mécanique
classique, une pour chaque dimension d’espace) associé à une base :
vecteurs i
r
; j
r
; k
r
(mais il peut y avoir d’autres manières de les noter,
x
u
r
;
y
u
r
;
z
u
r
, par exemple). Ces vecteurs, dit « vecteurs unitaires » car
leurs normes vaut 1, sont orthogonaux entre eux (à moins que vous ne
vouliez absolument vous compliquer la vie !)
Notation
Un vecteur v
r
ayant pour coordonnées 2 ; -5 et 4 signifie v
r
= 2 i
r
– 5 j
r
+
4 k
r
. Il peut s’écrire : v
r
(2 ; -5 ; 4) ou
−
4
5
2
v
r
Norme et coordonnées
Ne pas confondre le vecteur u
r
avec sa norme
222 zyx
uuuuu ++==
r
, ni
avec ses coordonnées u
x
, u
y
et u
z
.
La norme u de u
r
est toujours positive
Les coordonnées u
x
, u
y
et u
z
peuvent être positives ou négatives.
Opérations sur les vecteurs
Somme zwv
r
r
r
=+ : les coordonnées de z
r
sont la somme des
coordonnées de v
r
et w
r
.
z
x
= v
x
+ w
x
; z
y
= v
y
+ w
y
; etc.
Produit scalaire zwv =⋅
r
r
. z est un scalaire (un nombre) qui vaut :
z = v
x
· w
x
+ v
y
· w
y
+ v
z
· w
z
Dérivée d’un vecteur : La dérivée d’un vecteur )( tv
r
, notée t
tv
d
)(d
r
est un
vecteur dont les coordonnées sont les dérivées des coordonnées de )(tv
r
=
t
tv
t
tv
t
tv
t
tv
z
y
x
d
)(d
d
)(d
d
)(d
d
)(d
r
Équation vectorielle
Une équation vectorielle correspond à autant d’équations identiques
associées à chaque coordonnée des vecteurs.
Exemple : 2 u
r
+ v
r
= -5 w
r
signifique que :
2 u
x
+ v
x
= -5· w
x
; 2 u
y
+ v
y
= -5· w
y
, etc.
Exercice 3 Vecteurs
Ne jamais, jamais écrire qu’un vecteur est égal
à un nombre !
s
inon

TS www.pichegru.net 19 décembre 2016
-2-
C
C
Ci
i
in
n
né
é
ém
m
ma
a
at
t
ti
i
iq
q
qu
u
ue
e
e
Choisir un référentiel d’étude
Définir et reconnaître des mouvements (rectiligne uniforme, rectiligne
uniformément varié, circulaire uniforme, circulaire non uniforme) et
donner dans chaque cas les caractéristiques du vecteur accélération.
La cinématique est un endroit où l’on peut trouver des films est l’étude des
mouvements indépendamment des causes (forces) qui les produisent.
P Pr ré éa al la ab bl le es s
Définir le système étudié. Ce système sera, en Terminale, assimilé à un
simple point, qui est son centre d’inertie M. On ignorera les rotations que
l’objet peut éventuellement faire sur lui-même.
Définir le référentiel d’étude. Il s’agit d’un point de référence O par
rapport auquel se fait le mouvement. Souvent, il s’agit d’un point au sol.
Quelques référentiels
Définir le repère (axes des coordonnées) de manière à simplifier l’étude
du mouvement.
Si le mouvement est rectiligne , un seul axe (O x ) bien choisi suffit. Si le
mouvement est à deux dimensions, il faudra deux axes. Nous n’étudierons
pas de mouvement à trois dimensions en terminale.
G Gr ra an nd de eu ur rs s é ét tu ud di ié ée es s
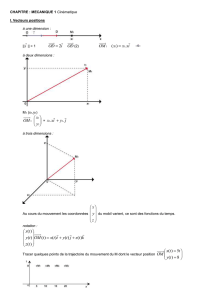
Vecteur position )(OM t qui définit la position de M dans le repère à
chaque instant.
Vecteur vitesse , tangent à la trajectoire, dans le sens du mouvement.
t
tv
d
OMd
)( ≡
r
Vecteur accélération
t
v
ta
d
d
)(
r
r≡
Remarque : le égal à trois barres signifie « égal par définition à ». C’est
donc une égalité qui est toujours vraie.
Vecteurs vitesse et accélération
D Di if ff fé ér re en nt ts s t ty yp pe es s d de e m mo ou uv ve em me en nt t
Définitions à connaître
Mouvements rectilignes
Uniforme (MRU) : ligne droite, v
r
constant, 0
r
r
=a.
Uniformément varié : en ligne droite, cte=a
r.
Exercice 4 Mouvement rectiligne uniforme
Mouvements circulaires
Dans le cas des mouvements circulaires, on se
place le plus souvent dans le repère de Frénet, qui
simplifie beaucoup les calculs.
Repère de Frénet : Vecteurs unitaires
t
u
r
tangent
à la trajectoire, dans le sens du mouvement et
n
u
r
orthogonal à la trajectoire, vers C.
Dans ce repère :
n
2
t
d
du
R
v
u
t
v
arrr +=
Mouvement circulaire uniforme : valeur de v constante
(attention cte≠v
r car ce vecteur change de direction au cours du temps),
donc :
n
2
u
R
v
arr =
Mouvements rectiligne et parabolique
Exercice 5 Mouvement circulaire uniforme
Exercice 6 La « passe en avant » au rugby
L
L
Le
e
es
s
s f
f
fo
o
or
r
rc
c
ce
e
es
s
s à
à
à c
c
co
o
on
n
nn
n
na
a
aî
î
ît
t
tr
r
re
e
e
F Fo or rc ce e d d’ ’a at tt tr ra ac ct ti io on n g gr ra av vi it ta at ti io on nn ne el ll le e
Deux corps A et B, pouvant être considérés comme ponctuels ou à
répartition sphérique de masse (en clair : de « petits » objets, ou des astres
à peu près sphériques), exercent l’un sur l’autre une force attractive.
2
B/AA/B
d
mmG
FF
BA
⋅⋅
==
m
A
et m
B
: masse des corps A et B (kg)
G : constante de gravitation universelle. 6,67·10
-11
m
3
·kg
-1
·s
-2
d : distance entre le centre des deux corps
La force qu’exerce un astre sur un objet à proximité de sa surface est
appelée le poids de cet objet. Si on reste « à proximité » de cet astre, on
voit que le poids d’un objet est proportionnel à sa masse : gmP
r
r
⋅=
Le vecteur g
r
est appelé champ de pesanteur. C’est un vecteur orienté vers
le centre de l’astre, qui est par définition vertical.
Gravity visualized
Exercice 7 Attraction gravitationnelle
R Ré éa ac ct ti io on n d d’ ’u un n s su up pp po or rt t
Lorsqu’un objet est posé sur un support (qu’il soit solide, ou liquide), ce
support exerce une force perpendiculaire à sa surface, orientée vers le haut,
sur cet objet, si cet objet est immobile.
Si l’objet n’est pas immobile, il s’exerce des forces de frottement entre le
support et l’objet. Selon les énoncés des exercices, cette force de
frottement est incluse dans la force de réaction, ou considérée comme une
force à part. Cela ne change rien à la résolution de l’exercice.
F Fo or rc ce e d de e f fr ro ot tt te em me en nt ts s
Les forces de frottement sont toujours opposées au sens du déplacement.
Elles dépendent de la vitesse de l’objet, ainsi que de nombreux autres
facteurs (nature du fluide, nature des surfaces en contact, forme de l’objet).
En première approximation, pour un solide donné se déplaçant dans un
fluide à une vitesse « pas trop élevée », la valeur de la force de frottement
est proportionnelle à la vitesse :
vkf
r
r
⋅−=
La prise en compte des forces de frottement complique grandement les
calculs. En Terminale, nous nous placerons dans des situations où ces
forces pourront être négligées.
P Po ou us ss sé ée e d d’ ’a ar rc ch hi im mè èd de e
Tout corps plongé dans un fluide subit une force verticale, orienté vers le
haut, dont la valeur est égale au poids du volume V de fluide déplacé .
gV
r
r
⋅⋅−=Π
fluide
ρ
La poussée d’Archimède peut être négligée si la densité de l’objet plongé
dans le fluide est très supérieur à la densité du fluide.
F Fo or rc ce e é él le ec ct tr ri iq qu ue e
Une charge électrique q placée dans un champ électrique subit une force :
EqF
r
r
⋅=
Rappels : Le champ électrique est orienté du (+) vers le (–).
Unité de la charge : coulomb (C)
Unité du champ électrique : V·m
-1
Repères et forces
A
B
B/A
F
r
A/B
F
r
G
P
r
R
r
Objet immobile
G
P
r
N
R
r
Objet en mouvement
v
r
f
r
R
r
C
t
u
r
n
u
r
R

TS www.pichegru.net 19 décembre 2016
-3-
L
L
Le
e
es
s
s 3
3
3 l
l
lo
o
oi
i
is
s
s d
d
de
e
e N
N
Ne
e
ew
w
wt
t
to
o
on
n
n
Connaître et exploiter les 3 lois de Newton
R Ré éf fé ér re en nt ti ie el l g ga al li il lé ée en n
Définition : référentiel dans lequel les 2 premières lois de Newton
s’appliquent (sera toujours le cas en terminale).
Un référentiel non galiléen serait un référentiel qui tourne ou accélère par
rapport à un référentiel galiléen.
n n° °1 1 : : P Pr ri in nc ci ip pe e d d’ ’i in ne er rt ti ie e
Si la somme des forces extérieures qui s’appliquent à un système est nulle,
alors ce système est en mouvement rectiligne uniforme ou immobile, et
réciproquement.
immobileou MRU0
ext
⇔=
∑
r
r
F
Un système isolé (qui ne subit aucune force extérieure) ou pseudo-isolé
(les forces extérieures se compensent) est en MRU ou immobile. La
réciproque est vraie.
Principe d’inertie
n n° °2 2 : : R Re el la at ti io on n f fo on nd da am me en nt ta al le e d de e l la a d dy yn na am mi iq qu ue e
(
(R RF FD D) )
amF
r
r
⋅=
∑
ext
Un objet soumis à des forces qui ne se compensent pas subit une
accélération.
Remarque 1 : la 1
ère
loi est incluse dans la deuxième.
Remarque 2 : cette expression n’est valable que pour un objet de masse
constante. Il existe une expression plus générale pour des objets dont la
masse varie.
Accélération
Curling avec et sans frottements
Exercice 8 Décollage du Rafale
Exercice 9 Balle lancée vers le haut
n n° °3 3 : : P Pr ri in nc ci ip pe e d de es s a ac ct ti io on ns s r ré éc ci ip pr ro oq qu ue es s
Si un objet A exerce sur un objet B une force
BA
F
→
r
, alors B exerce une
force sur A
AB
F
→
r
telle que :
ABBA
FF
→→
−=
r
r
Rebond d’une balle de golf
Exercice 10 Principe des actions réciproques
 Étudier un mouvement
Préalables
• Définir le système étudié ; choisir un référentiel et un repère.
• Faire un bilan des forces extérieures qui s’appliquent au système.
Appliquer la RFD
• Trouver le vecteur accélération a
r
grâce à la RFD.
• En déduire v
r
( intégration → constante).
• En déduire OM ( intégration → constante).
Intégration successive :
0 → constante → fonction affine (droite) → trinôme (parabole)
Interroger les équations
• Leur poser une question, qui dépend de l’exercice (au bout de combien
de temps l’objet touche le sol ? Au bout de combien de temps aura-t-il
atteint telle vitesse ? Au bout de quelle distance aura-t-il atteint telle
vitesse ?)
• Si vous traitez vos équations correctement (unités), elles vous répondront
correctement (mais uniquement ce qu’elles savent !).
 Convertir de m·s
-1
en km·h
-1
1 m·s
-1
= 3600 m·h
-1
car il y a 3600 s dans 1 h
3600 m·h
-1
= 3,6 km·h
-1
Donc : 1 m·s
-1
= 3,6 km·h
-1
Q
Q
Qu
u
ua
a
an
n
nt
t
ti
i
it
t
té
é
é d
d
de
e
e m
m
mo
o
ou
u
uv
v
ve
e
em
m
me
e
en
n
nt
t
t
Définir la quantité de mouvement d’un point matériel
D Dé éf fi in ni it ti io on n
La quantité de mouvement
p
r
d’un système est un vecteur définit par la
relation :
vmp
r
r
⋅≡
Remarque : p
système
= somme p éléments
C Co on ns se er rv va at ti io on n d de e l la a q qu ua an nt ti it té é d de e m mo ou uv ve em me en nt t
Système fermé : qui ne perd pas de matière.
Système isolé ou pseudo-isolé :
0
ext
r
r
=
∑
F
La quantité de mouvement d’un système fermé et isolé se conserve (ne
varie pas au cours du temps) dans un référentiel galiléen.
S Sy ys st tè èm me e o ou uv ve er rt t
Un système ouvert perd de la masse (fusée éjectant des gaz ou arme à feu
éjectant une balle).
Une force de poussée
e
v
t
m
Fr
r
d
d
p
−= apparaît.
Cette formule peut se comprendre à partir de l’expression générale de la
RFD : t
p
Fd
d
ext
r
r=
∑
Principe de la propulsion à réaction
Fonctionnement d’un moteur de fusée
Collision de deux chariots
 Étudier un choc entre deux objets
• Justifier que la quantité de mouvement totale du système {objet 1 ; objet
2} se conserve (système isolé et fermé).
• Calculer la quantité totale de mouvement avant le choc (ou avant le tir)
• La quantité totale de mouvement après le choc sera la même qu’avant.
TP 2.1 : Quantité de mouvement
Mettre en œuvre une démarche expérimentale pour interpréter un mode
de propulsion par réaction à l’aide d’un bilan qualitatif de quantité de
mouvement.
Objectif : Mettre en évidence la conservation de la quantité de
mouvement après un « tir ».
Technique(s) : Exploitation d’une vidéo avec le logiciel « Latis Pro».
Modélisation de mesure expérimentale.
Résultats : La quantité de mouvement des deux chariots mobiles a la
même valeur après leur séparation, bien qu’ils aient des masses et des
vitesses différentes. Seul le sens du vecteur change.
Conclusion : La conservation de la quantité de mouvement a été mise en
évidence.
Exercice 11 Ravitaillement de la station ISS
Exercice 12 Le rugby, sport de contact
M
M
Mo
o
ou
u
uv
v
ve
e
em
m
me
e
en
n
nt
t
ts
s
s d
d
da
a
an
n
ns
s
s u
u
un
n
n c
c
ch
h
ha
a
am
m
mp
p
p
u
u
un
n
ni
i
if
f
fo
o
or
r
rm
m
me
e
e
Mettre en œuvre les trois lois de Newton pour étudier des mouvements
dans des champs de pesanteur et électrostatiques uniformes
T Ty yp pe es s d de e m mo ou uv ve em me en nt t
Le mouvement d’une particule massique dans un champ de pesanteur
uniforme et le mouvement d’une particule chargée (électron, proton) dans
un champ électrostatique (c’est-à-dire un champ électrique constant)
uniforme ont un point commun : les particules qui y sont soumises
subissent une unique force constante , si, bien sûr, les frottements
peuvent être négligés.

TS www.pichegru.net 19 décembre 2016
-4-
Il en résulte que les équations de leur mouvement sont similaires. Elles
auront donc un mouvement ayant la même forme : rectiligne ou
parabolique .
Rappel de vocabulaire
Uniforme : identique en tous points de l’espace
Constant : identique au cours du temps
Chute libre : Un objet est en chute libre si la seule force qui s’exerce sur
lui est son poids. Cela signifie qu’il ne subit pas de frottement. En réalité,
un objet dans l’atmosphère n’est jamais en chute libre, à cause des forces
de frottement dues aux gaz. Mais lors des premiers instants de sa chute,
lorsque sa vitesse n’est pas encore importante, les frottements peuvent
souvent être négligés (sauf cas particuliers : un parachute, une
mongolfière, une plume, une feuille de papier).
Mouvement rectiligne
Le mouvement d’une telle particule sera rectiligne si sa vitesse initiale est
nulle , ou si le vecteur vitesse initial
0
v
r
est colinaire au vecteur champ
g
r
ou E
r
. Que le sens de
0
v
r
soit identique ou opposé au sens du vecteur
champ n’a pas d’importance. Le mouvement ne se fait que selon une
dimension , c’est-à-dire qu’une seule coordonnée du vecteurs position va
varier au cours du temps, si vous avez bien choisi votre repère.
Mouvement parabolique
Si les conditions du paragraphe précédent, portant sur le vecteur vitesse
initiale, ne sont pas respectées, alors le mouvement de la particule est
parabolique. Le mouvement se fait selon deux dimensions , c’est-à-dire
que deux coordonnées du vecteurs position vont varier au cours du temps,
si vous avez bien choisi votre repère.
Paramètres d’un mouvement parabolique
F Fo or rc ce es s e et t c ch ha am mp ps s
Poids (dans champ de pesanteur uniforme)
gmP
r
r
⋅=
Force électrique s’exerçant sur une charge dans un champ électrique.
EqF
r
r
⋅=
e
É Éq qu ua at ti io on ns s d du u m mo ou uv ve em me en nt t
Pour trouver les équations du mouvement, il vous suffit de suivre la
méthode indiquée au paragraphe « Lois de Newton ».
Mouvement rectiligne Mouvement parabolique
Accélération :
a
x
= 0
a
z
= – F/m
Accélération :
a
x
= 0
a
z
= – F/m
Vitesse :
v
x
= v
0 x
= 0
v
z
= –(F/m)·t + v
0 z
Vitesse :
v
x
= v
0 x
≠ 0
v
z
= –(F/m)·t + v
0 z
Position :
x = x
0
z = – ½ ·(F/m)·t
2
+ v
0z
·t + z
0
Position :
x = v
0 x
·t + x
0
z = –½· (F/m)·t
2
+ v
0z
·t + z
0
 Coordonnées d’un vecteur
Il vous sera parfois nécessaire de trouver les coordonnées d’un vecteur,
connaissant sa norme et l’angle qu’il fait avec un des axes du repère.
Il suffit pour cela d’utiliser correctement les sinus et les cosinus, en
prenant garde au signe des coordonnées.
w
x
= w·cos α ; w
z
= w·sin α ; m
x
= –m·sin γ ; m
z
= m·cos γ
TP 2.2 : Modélisation d’une trajectoire parabolique
Mettre en œuvre une démarche expérimentale pour étudier un
mouvement
Problématique : Quelles sont les caractéristiques de la trajectoire d’un
ballon lancé vers un panier ? Quelle est sa vitesse initiale et l’angle α que
fait
0
v
r
avec l’horizontale ?
Technique(s) : Exploitation d’une vidéo avec le logiciel Atelier
scientifique.
Démarche : Pointer les positions successives du ballon. Modéliser sa
trajectoire. Tracer l’allure des graphiques représentant a
x
(t), a
y
(t)
,
v
x
(t),
v
y
(t)
Résultats : La trajectoire du ballon est parabolique. Sur l’axe horizontal
Ox, l’accélération a
x
est nulle, la vitesse v
x
est constante. Sur l’axe vertical
Oy, l’accélération a
y
vaut -9,8 m·s
-2
et la vitesse v
y
est une droite
décroissante de pente -9,8 m·s
-2
.
La vitesse initiale du ballon v
0
=
2
y0
2
x0
)()( vv + ≅ 7 m·s
-1
et arctan α =
arctan (v
0y
/v
0x
) ≅ 50º.
Exercice 13 Le rugby, sport d’évitement
Exercice 14 Service au tennis
Exercice 15 Rapport e/m de l’électron
O
O
Or
r
rb
b
bi
i
it
t
te
e
es
s
s
Connaître les trois lois de Kepler ; exploiter la 3ème loi dans le cas
d’un mouvement circulaire
M Mo ou uv ve em me en nt t g gé én né ér ra al l : : l l’ ’e el ll li ip ps se e
Un corps C en orbite autour d’un corps O beaucoup plus massif que lui
possède un mouvement elliptique . Une orbite circulaire n’est qu’un cas
particulier d’orbite.
Remarque : un cercle est une ellipse particulière, de même qu’un carré est
un rectangle particulier.
L Lo oi is s d de e K Ke ep pl le er r
Kepler, (1571-1630), a établi ces trois lois empiriquement, uniquement
grâce à ses observations et à des éphémérides. Elles se démontrent
néanmoins mathématiquement et sont des conséquences des trois lois de
Newton (qui n’ont été découvertes qu’après sa mort).
Si un corps C orbite atour d’un corps O beaucoup plus massif que lui
(schéma ci-dessus), alors :
• Loi n°1 (loi des orbites) : O occupe un des foyers de l’ellipse.
• Loi n°2 (loi des aires) : Pendant des intervalles de temps égaux, les aires
balayées par OC sont égales. (Si le corps C a mis le même temps pour
passer de la position C
0
à C
1
et de C
2
à C
3
, alors les surfaces S
1
et S
2
sont
égales).
• Loi n°3 (loi des périodes) : La période de révolution T est liée à la
valeur du demi grand axe a :
O
2
3
2
π4
MG
a
T⋅
=
G = 6,67·10
-11
m
3
·kg
-1
·s
-2
.
M
O
: masse de l’astre O
Lois de Kepler
Paramètres de mise en orbite d’un satellite
O
C
0
F
1
F
2
A P
C
1
C
2
C
3
S
1
S
2
Demi grand axe a
O
z
x
F
r
0
v
r
O
z
x
F
r
0
v
r
O
z
x
w
r
α
m
r
γ

TS www.pichegru.net 19 décembre 2016
-5-
C Ca as s p pa ar rt ti ic cu ul li ie er r : : M Mo ou uv ve em me en nt t c ci ir rc cu ul la ai ir re e
Démontrer que, dans l’approximation des trajectoires circulaires, le
mouvement d’un satellite, d’une planète est uniforme. Établir l’expression
de sa vitesse et de sa période.
Si une planète ou un satellite possède un mouvement circulaire autour de
son astre attracteur, il s’en suit obligatoirement que son mouvement est
uniforme .
Ceci se démontre facilement et vous devez savoir refaire cette
démonstration, car c’est une question qui revient souvent dans les
épreuves du bac.
Démonstration en trois points
Supposons qu’un satellite B ait un mouvement
circulaire autour d’une planète A, cette dernière
étant le centre de sa trajectoire circulaire (1
ère
loi
de Kepler). Donc, dans le repère de Frenet, le
vecteur
n
u
r
, qui est par définition perpendi-
culaire au vecteur
t
u
r
, pointe vers le centre de la
planète.
• Direction et sens de la force qui s’exerce sur
le satellite :
Le satellite n’est soumis qu’à la force gravitationnelle de cette planète, qui
pointe vers le centre de celle-ci (loi de la gravitation universelle) et donc la
force
BA→
F
r
que la planète exerce sur le satellite est uniquement selon le
vecteur
n
u
r
(ce serait pas le cas si le mouvement n’était pas circulaire !)
• Direction et sens de l’accéleration du satellite
BA→
F
r
est la seule force qui s’exerce sur le satellite. Donc la RFD nous
donne, dans ce cas, amF
r
r
⋅=
→ BBA
. Ceci implique que l’accélération du
satellite est aussi uniquement selon le vecteur
n
u
r
• Identification de l’expression de l’accéleration donnée par la RFD
avec l’expression de l’accéleration dans un repère de Frenet
Dans un repère de Frenet, nous avons vu que a
r
peut s’écrire
nt
u
r
v
u
t
v
a
rrr
2
d
d+= . Or, d’après la RFD, l’accélération ne possède qu’une
composante selon
n
u
r
. Donc le terme t
v
d
d est nul. La valeur de la vitesse
du satellite est donc constante. CQFD.
Vitesse du satellite
À partir des relations
n
2
u
r
v
a
rr
=(Frenet) et
n
2
A
B
BA
u
r
mG
m
F
ar
r
r⋅
⋅
==
→
, on
obtient :
r
mG
vA
⋅
=
Période du satellite
La période T du satellite est la durée nécessaire pour que le satellite
effectue une révolution complète, donc parcourt le périmètre de son orbite,
soit 2 πr .
Vu que la vitesse est constante, on peut écrire T = 2 πr / v . D’où on
obtient :
A
π2
mG
r
rT
⋅
⋅⋅=
Exercice 16 La mission Planck
Exercice 17 Station ISS
Exercice 18 Étude du mouvement du satellite Ibuki
Exercice 19 Étude de l’orbite de Hubble
Exercice 20 Satellite géostationnaire
TP 2.3 : Détermination de la masse de Sagittarius A*
Objectif : Déterminer la masse du trou noir central de notre galaxie.
Démarche : À partir d’une série de photos prises par Hubble entre 1992 et
2002, on étudie les caractéristiques de l’orbite d’une étoile autour du trou
noir Sagitarius A* (période et grand axe de l’ellipse). Puis, en utilisant la
3
ème
loi de kepler, on calcule la masse de ce trou noir.
Résultats : Cette masse vaut environ 1,5·10
6
masses solaire (valeur
estimée par les chercheurs : entre 2 et 3 millions de masses solaire).
É
É
Én
n
ne
e
er
r
rg
g
gi
i
ie
e
e m
m
mé
é
éc
c
ca
a
an
n
ni
i
iq
q
qu
u
ue
e
e
Analyser les transferts énergétiques au cours d’un mouvement d’un
point matériel.
Généralités sur l’énergie
É Én ne er rg gi ie e c ci in né ét ti iq qu ue e
2
C
2
1
vmE ⋅=
m : masse en kg
v : vitesse en m·s
-1
La vitesse d’un objet dépendant du référentiel choisi, on voit donc que
l’énergie cinétique d’un objet dépend également du référentiel choisi.
Exercice 21 Énergie cinétique
É Én ne er rg gi ie es s p po ot te en nt ti ie el ll le es s
Énergie potentielle de pesanteur
.E
PP
= m · g · z.
m : masse en kg
g : intensité de la pesanteur en N·kg
-1
z : altitude en m
L’énergie potentielle de pesanteur dépend du choix de l’origine des
altitudes et donc du repère choisi. Mais ce n’est pas un problème car ce qui
nous intéresse est la variation de cette énergie potentielle, qui elle ne
dépend pas de l’origine des altitudes.
Exercice 22 Énergie potentielle de pesanteur
Énergie potentielle électrique
.E
PE
= q · V.
q : charge en coulomb (C)
V : potentiel électrique en volt (V)
Le potentiel électrique est à l’interaction électromagnétique ce que la
hauteur est à l’interaction gravitationnelle.
Une différence de potentiel (ddp), c’est-à-dire une tension, correspond à
une différence de hauteur.
Un champ électrique est une grandeur vectorielle, orientée de + vers le –
et dont la valeur, exprimée en V·m
-1
, exprime l’intensité de la variation du
potentiel électrique dans l’espace.
L’énergie potentielle électrique dépend du choix de l’origine des
potentiels. Mais ce n’est pas un problème car ce qui nous intéresse est la
variation de cette énergie potentielle, qui, elle, ne dépend pas de l’origine
des potentiels électriques.
Exercice 23 Énergie potentielle électrique
 Variation d’une grandeur
La variation d’une grandeur, quelle qu’elle soit, vaut :
Valeur finale – Valeur initiale
É Én ne er rg gi ie e m mé éc ca an ni iq qu ue e
L’énergie mécanique E
M
d’un système est la somme de son énergie
cinétique et de ses énergies potentielles.
∑
+=
PCM EEE
TP P2.4 : Énergie mécanique d’un objet en chute
libre
Problématique : Comment évolue l’énergie mécanique d’un objet au
cours d’une chute libre ?
Technique(s) : Exploitation d’une vidéo avec Latis Pro .
Démarche : Pointer les positions successives du ballon. Modéliser sa
trajectoire. En déduire les graphiques montrant E
C
( t ), E
PP
( t ) et E
M
( t )
Résultats : Au cours de la trajectoire parabolique du ballon, l’énergie
mécanique se conserve
A
t
u
r
n
u
r
BA→
F
r
B