n°8 p 175 a. Dans le référentiel (terrestre) de la patinoire, considéré

n°8 p 175
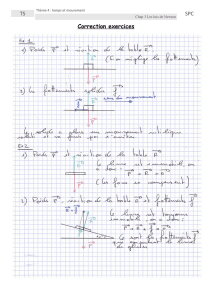
a. Dans le référentiel (terrestre) de la patinoire, considéré comme galiléen, on étudie le système constitué par les
deux patineurs.
b. - Avant qu’ils ne se repoussent, les patineurs sont immobiles, leur quantité de mouvement est nulle. La
quantité de mouvement du système est alors nulle :
⃗p=⃗ 0
.
- Lorsque A et B se sont repoussés, la quantité de mouvement du système est :
⃗
p'= ⃗ pA+ ⃗ pB
.
- Les frottements étant négligeables, chaque patineur est soumis à deux forces qui se compensent, son
poids et la réaction du sol : le système est isolé. Dans ce cas, il y a conservation de la quantité de
mouvement :
⃗p=
⃗
p'
, soit
⃗
0= ⃗ pA+ ⃗ pB
.
Les vecteurs quantité de mouvement de A et de B sont alors opposés :
⃗ pA=− ⃗ pB
.
c. L’égalité précédente se traduit par :
mA ⃗ vA=−mB ⃗ vB
soit
⃗
vB=− mA
mB
⃗
vA
.
Les vecteurs vitesse ont même direction mais des sens opposés.
Si vA = 4,0 m×s-1,
vB=− 50
80
×4,0
= 2,5 m×s-1 .
n°17 p 178
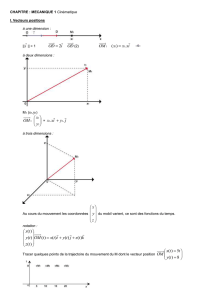
a. x(t) = 1,5t.
b.
vx=dx
dt
= 1,5 m.s-1 ;
vy=dy
dt
= 0, car y(t)= cte =1 m.
c. Le vecteur vitesse est un vecteur constant, la
trajectoire est une droite et le mouvement est rectiligne
uniforme.
n°19 p 175
a. Le mouvement est rectiligne uniforme si le vecteur vitesse est un vecteur constant (la trajectoire est une droite
et la valeur de la vitesse est constante).
Le mouvement du parachutiste est rectiligne uniforme dans le référentiel terrestre.
b. Le système {parachutiste+parachute} est soumis à son poids
⃗
P
et aux frottements de l'air
⃗
F
.
c.
⃗
P
: direction : verticale
sens : vers le bas
norme : P = mg =
90×9,8
= 8,8.102 N.
D'après le principe d'inertie, et puisque le mouvement du système est rectiligne uniforme, les forces
⃗
P
et
⃗
F
se compensent :
⃗
P+⃗ F=⃗ 0
.
Alors,
⃗
F
: direction : verticale
sens : vers le haut
norme : F = P = 8,8.102 N.
d. La vitesse du système est constante, on peut calculer la vitesse moyenne :
v=d
t
=400
90
v = 4,4 m.s-1 .