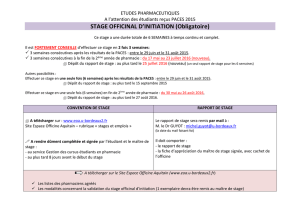
Cours Mathématiques PACES UHP-Nancy

Cours Mathématiques PACES UHP-Nancy
V. Latocha
PACES UHP
septembre 2010
remerciements à D. Schmitt et V. Ries
V. Latocha (PACES UHP) Cours mathématiques Paces septembre 2010 1 / 48

1Fonctions d’une variable réelle
Rappel sur la continuité
Dérivation
Fonctions usuelles
V. Latocha (PACES UHP) Cours mathématiques Paces septembre 2010 2 / 48

1Fonctions d’une variable réelle
Rappel sur la continuité
Dérivation
Fonctions usuelles
V. Latocha (PACES UHP) Cours mathématiques Paces septembre 2010 3 / 48

Soient Iun intervalle de R,fune application de Idans Ret aun point de
I.
Définition
La fonction fest dite continue au point a si et seulement elle admet une
limite en ce point et cette limite est f(a)
lim
x→af(x) = f(a).
V. Latocha (PACES UHP) Cours mathématiques Paces septembre 2010 4 / 48

Définition
On dit qu’une fonction fest continue sur Isi et seulement si elle est
continue en tout point ade I.
à noter
La notion de continuité d’une fonction fa pour objet de traduire
mathématiquement le fait que sa courbe représentative peut se tracer sans
"lever le crayon".
V. Latocha (PACES UHP) Cours mathématiques Paces septembre 2010 5 / 48