Correction exercice méthode d`Euler

Correction exercice méthode d’Euler
1) Mouvement sans frottement
-a- -b- P = ρ × V × g et ΠA = ρair × V × g
d’où :
Aair
Pρ2
ρ1, 2
==
Π= 1,7
donc la poussée d’Archimède n’est pas négligeable.
-c- Dans le référentiel terrestre considéré comme galiléen,
appliquons la 2ème loi de Newton au système {ballon}.
ext
Fma
=
⋅
∑r
r
s’écrit, en projections sur l’axe (Oz) :
P - ΠA = ma, soit ρVg - ρair Vg = ρVa.
Donc air
ρ
a=g 1- ρ
⎛⎞
⎜⎟
⎝⎠
= 3,9 m.s-2.
-d- Par définition, dv
a= dt donc v(t) est une primitive de l’accélération a = Cte.
v(t) = a⋅t + v0 . Comme la vitesse initiale est nulle, on a v(t) = a⋅t
Comme dz
v= dt , on en déduit z(t) = 2
1at
2.
-e- Pour z = 5 m on a t = 2z 10
a3,9
== 1,6 s.
On reporte dans v(t) : v(1,6) = 3,9×1,6 = 6,2 m.s-1
-f- L’accélération est constante et dans le sens du mouvement, donc il s’agit d’un mouvement
rectiligne uniformément accéléré.
2) Equation différentielle du mouvement
-a- -b- La 2ème loi de Newton s’écrit maintenant :
P - ΠA – f = ma
Soit
()
air
ρρ Vg kv = m a−−
En divisant par m :
(
)
air
ρρVg kv
a= mm
−−
-c- On a m = ρV, d’où :
()
air
ρρgkv
a= ρm
−− soit : air
ρ
dv kv
a=1 g
dt ρm
⎛⎞
=−−
⎜⎟
⎝⎠ .
P
A
Π
r
P
O
z
P
A
Π
r
P
O
z
f

3) Résolution
-a- à t = 0, v = 0 donc a(0) = g(1-ρair / ρ) = 3,9 m.s-2.
-b- v(0,1) = v(0) + 0,1×a(0) = 0 + 0,1×3,9 = 0,39 m.s-1.
-c- a(0,1) = air
ρk
1gv(0,1)
ρm
⎛⎞
−−
⎜⎟
⎝⎠ = 3,9 - 3×0,39 = 2,73 m.s-2.
-d- a(0,3) = air
ρk
1gv(0,3)
ρm
⎛⎞
−−
⎜⎟
⎝⎠ = 3,9 - 3×0,85 = 1,35 m.s-2.
v(0,4) = v(0,3) + 0,1×a(0,3) = 0,85 + 0,1×1,35 = 0,985 m.s-1.
e- La vitesse limite vlim est atteinte lorsque a = 0.
Soit air
lim
ρ
kvg1
mρ
⎛⎞
=⋅−
⎜⎟
⎝⎠
d’où air
lim
ρ
mg
v1
kρ
⎛⎞
=⋅−
⎜⎟
⎝⎠
= 1,31 m.s-1.
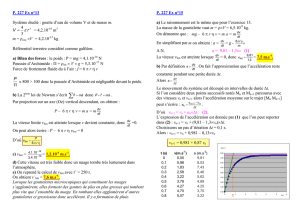
-g-
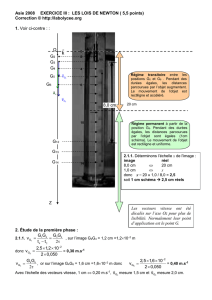
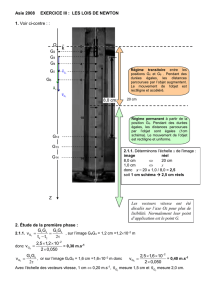
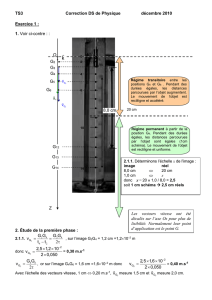
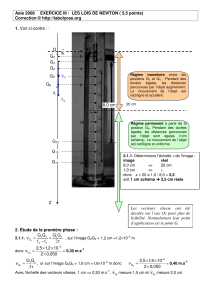
-h- Graphiquement : τ = 0,3 s.
Régime
transitoire
Régime
permanent
τ