Fiche méthodologique Notions sur les fonctions

Fiche méthodologique Notions sur les fonctions convexes
BCPST Lycée Hoche Pelletier Sylvain
CC
BY: $
\
=
Pour illustrer le théorème des accroissements finis on démontre ici quelques propriétés des fonctions
convexes. Un seul résultat est au programme : une fonction convexe est au-dessus de ses tangentes.
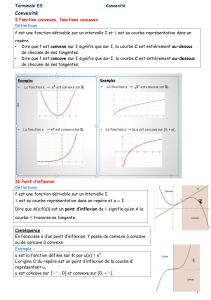
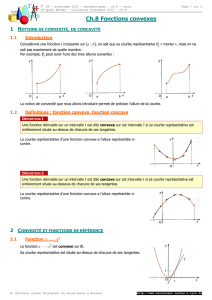
Définition 1. On dit que la fonction fest convexe sur un intervalle I, si :
∀(x, y)∈I2,∀λ∈[0,1], f (λx + (1 −λ)y)6λf (x) + (1 −λ)f(y).
Ainsi, la courbe représentative d’une fonction convexe est en dessous de toutes ses cordes.
Définition 2. On dit que la fonction fest concave sur un intervalle I, si :
∀(x, y)∈I2,∀λ∈[0,1], f (λx + (1 −λ)y)>λf (x) + (1 −λ)f(y).
Ainsi, la courbe représentative d’une fonction convexe est au dessus de toutes ses cordes.
Remarque:
– On voit que fest concave si et seulement si −fest convexe.
– La notion de convexité n’est utile que si fest définie sur un intervalle : il faut que (λx + (1 −λ)y)
soit élément de l’ensemble de définition de f.
– Dans la définition, on peut toujours supposer que x6y, et même x < y.
Exemple:
– une fonction affine est convexe et concave,
–x7→ x2est convexe,
– ln est concave, alors que exest convexe.
⋆Lien avec la dérivée
Dans le cas où fest dérivable, la dérivée est alors croissante.
Proposition 1. Soit fdérivable sur un intervalle I. On a alors :
fest convexe sur I⇐⇒ f′est croissant sur I
Démonstration. ⇒On suppose fconvexe et soit x < y deux éléments de I. On va comparer f′(x) et f′(y)
au taux de variation entre xet y,i.e. à : f(y)−f(x)
y−x. On a :
f′(x) = f′
d(x) = lim
z→x+
f(z)−f(x)
z−x= lim
λ→0+
f(λx + (1 −λ)y)−f(x)
λx + (1 −λ)y−x
En posant z=λx + (1 −λ)y,i.e. λ=z−y
x−y.
On a puisque fest convexe :
f(λx + (1 −λ)y)−f(x)
λx + (1 −λ)y−x=f(λx + (1 −λ)y)−f(x) (1 −λ)(y−x)
6λf (x) + (1 −λ)f(y)−f(x)
(1 −λ)(y−x)
=(1 −λ)(f(y)−f(x))
(1 −λ)(y−x)
=f(y)−f(x)
y−x
1

ainsi, f′(x)6f(y)−f(x)
y−x. Tandis que :
f′(y) = f′
g(x) = lim
z→y−
f(z)−f(y)
z−y= lim
λ→1−
f(λx + (1 −λ)y)−f(y)
λx + (1 −λ)y−y
On a puisque fest convexe :
f(λx + (1 −λ)y)−f(y)
λx + (1 −λ)y−y=f(λx + (1 −λ)y)−f(y) λ(x−y)
>λf (x) + (1 −λ)f(y)−f(y)
λ(x−y)
=λ(f(x)−f(y))
λ(x−y)
=f(x)−f(y)
x−y
Ainsi,
f′(x)6f(y)−f(x)
y−x6f′(y).
Ce qui prouve que f′est une fonction croissante.
⇐Supposons f′croissante soit x, y ∈I, et λ∈[0,1]. La propriété est évidente pour λ= 0 et λ= 1,
on suppose donc λ∈]0,1[. De même le cas x=yn’est pas intéressant, on suppose donc x < y.
Soit z=λx + (1 −λ)y. On a d’après le théorème des accroissements finis :
∃c∈]x, z[, f (z) = f(x) + f′(c)(z−x) = f(x) + f′(c)(1 −λ)(y−x)
∃d∈]z, y[, f (z) = f(y) + f′(d)(z−y) = f(y)−f′(d)λ(y−x)
f′est croissante, donc on a f′(c)6f′(d), donc en faisant λl1+ (1 −λ)l2.
f(z) = λf (x) + (1 −λ)f(y) + λ(1 −λ)(y−x)f′(c)−f′(d)
|{z }
60
6λf (x) + (1 −λ)f(y)
Et donc fest convexe.
⋆Cas d’une fonction deux fois dérivable
Proposition 2. Soit fdeux fois dérivable sur un intervalle I. Alors fconvexe si et seulement si f′′ >0
sur I.
De la même manière fest concave si et seulement si f′′ 60sur I.
Démonstration. Puisque fest deux fois dérivable, f′est croissant si et seulement si f′′ >0.
⋆Position de la courbe par rapport à la tangente
Une autre manière de voir : si fest une fonction convexe la courbe représentative Cfest en dessous
de la tangente :
Proposition 3. Soit fune fonction définie et dérivable sur un intervalle I. Alors fest convexe, si et
seulement si :
∀(a, x)∈I2, f (x)>f(a) + (x−a)f′(a)
i.e. fest au-dessus de sa tangente en apour tout a.
2

Démonstration. ⇒Supposons fconvexe et soit xet aéléments de I.
On sait que f′est croissant, et on sait que ∃c∈]a, x[, ou ]x, a[f(x) = f(a) + f′(c)(x−a).
Si x > a, on peut alors majorer f′(c) par f′(a) (car f′est croissant), comme (x−a)>0, on obtient :
f(x)>f(a) + (x−a)f′(a).
Si a > x on a alors f′(c)< f ′(a) et (x−a)60, et donc on obtient de nouveau : f(x)>f(a)+(x−a)f′(a).
⇐Soit xet yéléments de I, avec x < y on va démontrer que f′(x)6f′(y), i.e. la croissance de f′.
On a : f(x)>f(y) + (x−y)f′(y) donc : f′(y)>f(x)−f(y)
x−yet : f(y)>f(x) + (y−x)f′(x) donc :
f′(x)6f(y)−f(x)
y−x. D’où
f′(x)6f(y)−f(x)
y−x6f′(y).
⋆Conclusion
Ainsi, pour une fonction fdérivable sur Iet sa courbe représentative C, est équivalent :
(1) fconvexe,
(2) Cest en dessous de ces cordes,
(3) Cest au dessus de ses tangentes,
(4) f′est croissant,
(5) f′′ est positive (si deux fois dérivable).
C’est l’application des fonctions convexes en BCPST : pour montrer qu’une courbe représentative Cfest
au-dessus de ses tangentes, on montre que la fonction fest convexe. Pour cela, on montre simplement que
f′′ >0.
Remarque: Autre manière de voir : si fest C2, on peut appliquer Taylor-Lagrange à l’ordre 2. On
obtient alors :
∀a∈I, ∀x∈I, ∃c∈I , f (x) = f(a) + (x−a)f′(a) + (x−a)2f′′(c)
2.
Donc si f′′ est positive, on est sûr que (x−a)2f′′(c)>0 et donc : f(x)>f(a) + (x−a)f′(a). On retrouve
le fait que si f′′ >0, Cfest au-dessus de ses tangentes.
Comme application de la convexité il y a les approximations que l’on peut obtenir en comparant la
courbe à ses tangentes et/ou à ses cordes.
Application 1 Étudier la concavité de la fonction sinus sur [0, π], et en déduire que :
∀x∈0,π
22 πx6sin x6x.
On a aussi la définition :
Définition 3. Soit fune fonction définie et deux fois dérivable sur l’intervalle I, et aun élément de
I, qui n’est pas une extrémité de I. On dit que le point (a, f (a)) est un point d’inflexion de la courbe
représentative de fsi f′′ s’annule et change de signe en a.
L’intérêt est qu’avant a, la fonction est convexe tandis qu’après elle est concave. Donc la courbe C
traverse sa tangente au point a.
3