Question 1 - Moodle Poly Mtl

1
Question 1
Strat´egie: Probl`eme de cin´ematique dans le plan. Utilisation de la m´ethode du point de
contact (E). Calcul de la vitesse et de l’acc´el´eration relative du point Cdans un rep`ere
tournant (on attache un rep`ere tournant sur la pi`ece AOD).
C
F
O
D
E
30º 30º
225 mm
=C
Cvrel
vE = ω X rE/O
30º
vC
ω X(ω X rE/O)
2ω Xvrel
α X rE/O
arel
=
C
30º
aC
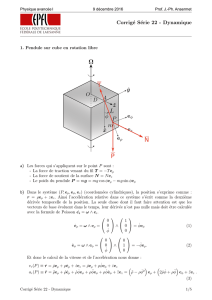
Figure 1: cin´ematique – diagrammes de vitesse et d’acc´el´eration
Cin´ematique des vitesses:
Calcul de la vitesse du point de contact vE:
vE“ωAOD rOE “p7qp0.225q
cos 30˝“1.8187 m{sŒ
Calcul de la vitesse relative vrel:
vEsin 30˝“vrel cos 30˝ñvrel “vE
?3“1.05 m{sÖ
Calcul de la vitesse vCdu piston CF .
vC“vEcos 30˝`vrel sin 30˝“ p1.8qcos 30˝` p1.0392qsin 30˝“2.1 m{sÓ
Cin´ematique des acc´el´erations:
Composantes de l’acc´el´eration de Cdans le rep`ere tournant:
Acc´el´eration angulaire de AOD:|αˆrE{O| “ p28q´0.225
cos 30˝¯“7.2746 m{s2Œ
Acc´el´eration de Coriolis de C:|2ωˆvrel| “ 2p7qp1.05q “ 14.7 m{s2Ô
Acc´el´eration centrip`ete de C:|ωˆpωˆrE{Oq| “ p1.8187q2´cos 30˝
0.225 ¯“12.731 m{s2Ö
Calcul de l’acc´el´eration aCdu piston CF . On prends la projection des acc´el´erations sur
un axe perpendiculaire `a OED:
aCcos 30˝“ |2ωˆvrel| ´ |αˆrE{O|
aC“ p14.7´7.2746q2
?3“8.5741 m{s2Ò
Calcul de l’acc´el´eration relative arel (grandeur et direction) de la goupille C par rapport
la rainure. On prends la projection des acc´el´erations sur l’axe OED:
aCsin 30˝“arel ´ |ωˆ pωˆrE{Oq|
arel “ p8.5741qp0.5q ` p12.731q “ 17.018 m{s2Õ

2
Question 2
Strat´egie: Probl`eme de cin´etique d’un m´ecanisme dans le plan vertical. D´emembement
du syst`eme en 2 pi`eces et utilisation du principe d’´equilibre dynamique (DCL=DCE).
Le centre de masse de la roue est situe au point A. Ce point suit un mouvement circulaire
autour du point O(rayon ℓ).
HO=IO αOA
mrOGωΟΑ2
O O
A
A
FAt
mg
FO
n
t
mrOGαΟΑ
Mg
FAt
FZt
Ml
Z
A
θ
θ
θ
DCL1
DCL2
DCE1
DCE2
Z
HA=IA αA
G
FZn
FAn
FAn
G
αΟΑ
Ml
ωΟΑ2
Figure 2: DCL et DCE
(a) Cin´etique du lien rigide OA, Relations d’´equilibre sur DCL1=DCE1:
ÿMO“IOαOA :´FAt ℓ`mg¯rOG cos θ“IOαOA
(b) Cin´etique de la roue A, Relations d’´equilibre sur DCL2=DCE2:
¯
IA“MR2
ÿMZ“¯
IAαA:´FAt R´MgR cos θ“ ´¯ IAαA´MRℓαOA “ ´MR pRαA`ℓαOAq
(c) Contrainte de vitesse et acc´el´eration angulaire au point A:
vA“ωOA ℓ“ωARet paAqt“αOA ℓ“αAR
En combinant les relations (a), (b) et (c) de fa¸con `a ´eliminer les variables FAt et αA, on
trouve: pm¯rOG `Mℓqgcos θ“`IO`2Mℓ2˘αOA
On utilise la relation de d´erivation en chaine
ωOA dωOA “αOA dθOA
et on int`egre de 0 `a π{2:
`IO`2Mℓ2˘żωOA
0
ω1
OAdω1 OA “ pm¯rOG `Mℓqgżπ{2
0
dθOA cos θOA
`IO`2Mℓ2˘ω12
OA
2ˇˇˇˇ
ωOA
0“ pm¯rOG `Mℓqgsin θOAˇˇˇ
π{2
0

3
La vitesse angulaire finale en position θOA “π{2 est donc:
ωOA “d2pm¯rOG `Mℓqg
IO`2Mℓ2
Application num´erique:
IO“ p3qp0.35q2“0.3675 kg ¨m2
ωOA “d2rp3qp0.3q ` p4qp0.5qsp9.81q
p0.3675q ` p2qp4qp0.5q2“4.9023 rad{s
vA“ωOA ℓ“ p4.9023qp0.5q “ 2.4512 m{s

4
Question 3
Strat´egie: Conservation de l’´energie m´ecanique entre la position 1 et la position 2.
30º
100 mm
l
6 kg
2 kg
200 mm
Oplan de référence
Figure 3: Position 1 du solide rigide
Calcul de la longueur de la barre (ℓ):
ℓ“2p0.2qcos 30˝“0.3464 m
Calcul du moment d’inertie massique de l’assemblage par rapport l’articulation (O):
IO“¯ Idisk ``¯ Ibar `md2˘
avec
¯
Idisk “1
2Mr2
disk et ¯
Ibar “1
12mℓ2
Donc:
IO“1
2p6qp0.2q2`ˆ1 12p2qp0.3464q2` p2qp0.1q2˙“0.16 kg ¨m2
Conservation de l’´energie m´ecanique:
Vg1“Vg2`T2
p2qp9.81qp0.1q “ ´p2qp9.81qp0.1q ` 1
2p0.16qω2
2ñω2“7.004 rad{s