Trigonométrie dans un triangle rectangle

Chapitre X Trigonométrie dans le triangle rectangle
Activité : à l'aide du logiciel Geogebra.(enregistré dans le dossier
travail)
Rappel :
Dans l'activité on a remarqué que pour un angle aigu donné dans un
triangle rectangle, le rapport du côté adjacent à l'angle donné et de
l'hypoténuse est constant. On a vu en 4ème que ce rapport constant ne
dépend que de la valeur de l'angle et qu'on l'appelait le cosinus de
l'angle.
Maintenant on observe que le rapport du côté opposé à l'angle et de
l'hypoténuse est lui aussi constant (on l'appellera le sinus de l'angle)
Et enfin on observe aussi que le rapport du côté opposé et de du côté
adjacent est lui aussi constant, il s'appellera la tangente de l'angle.
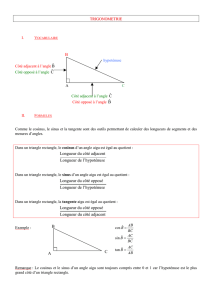
BA
CDans un triangle rectangle, le côté en
face de l'angle droit s'appelle
l'hypoténuse
Le côté BA est adjacent à l'angle en A
Il est aussi opposé à l'angle en C
Le côté BC est opposé à
l'angle en A.
Il est aussi adjacent à l'angle
en C.

I Lignes trigonométriques
3 formules s'annoncent grâce à l'activité ... écrivons les!
cos Â=longueur du côté ADJACENT à l ' angle Â
longueur del ' HYPOTENUSE =AB AC
sin Â=longueur du côté OPPOSE à l ' angle Â
longueur del ' HYPOTENUSE =BC AC
tan Â=longueur du côté OPPOSE à l ' angle Â
longueur du côté ADJACENT à l ' angle  =CB AB
L'angle aigu s'exprime en degrés.
Le cosinus d'un angle aigu est un nombre toujours compris entre 0 et
1.
Le sinus d'un angle aigu est un nombre toujours compris entre 0 et 1.
La tangente d'un angle aigu est un nombre positif.
Attention on calcule le cosinus, ou le sinus ou la tangente d'un angle
aigu dans un triangle rectangle nécessairement.
Voici une astuce mnémotechnique pour retenir les 3 formules :
SOH CAH TOA ou CAH SOH TOA
S pour Sinus
C pour Cosinus
T pour Tangente
O pour Opposé
A pour Adjacent
H pour Hypoténuse
II Trigonométrie et calculatrices
Attention, il faut toujours veiller à ce que la calculatrice soit en mode
degré (et non en mode radian qui est une autre unité d'angle)
1) Pour trouver la valeur du cosinus d'un angle aigu (ou du sinus ou
de la tangente)
tan 30°≈0,577
cos(60°)=0,5

sin 45 °≈0,707
attention aux signe environ égal si la valeur n'est pas exacte
(dans ce cas on donne en général 3 décimales)
2) Pour trouver la mesure de l'angle en degré dont on connait le
cosinus (ou le sinus ou la tangente)
Trouver la mesure de l'angle aigu qui a
pour cosinus 0,5, c'est 60°
pour sinus 0,658 c'est environ 41°
pour sinus 1,5 IMPOSSIBLE car
supérieur à 1
pour tangente 1 on trouve 45°
III Utilisation des lignes trigonométriques
1) Pour trouver la longueur d'un côté dans un triangle rectangle
Les données : « 1 côté et 1 angle » permettent de trouver la
mesure d'un autre côté
Exemples :
a) Dans le triangle ABC rectangle en B on sait que AB= 5 cm
et l'angle de sommet C mesure 45 ° Trouver AC
dessin à main levée codé (indiquer ce que l'on cherche en
couleur)
Puisque le triangle est rectangle en B, je peux utiliser la trigonométrie.
sin  C=AB
AC
Je remplace par les valeurs connues
sin 45°=5
AC
(
sin 45 °
1
=5
AC
¿
)
grâce à une 4ème proportionnelle on trouve
AC=1×5
sin 45°≈7,07cm
b) Dans le triangle DEF rectangle en D, on sait que DF=4 cm
et l'angle de sommet F mesure 30° Trouver DE
(faire le dessin à main levée)
Dans le triangle DEF rectangle en D, j'utilise la trigonométrie
tan  F=DE
DF

En remplaçant par les valeurs connues :
tan 30°=DE
4
Donc
DE=4×tan 30°
1
≈2,31cm
2) Pour trouver la mesure d'un angle aigu dans un triangle
rectangle
Les données : 2 côtés permettent de trouver la mesure d'un angle
aigu
Exemple1 : Dans le triangle BOY rectangle en Y, BO= 5 cm et
OY= 4 cm, trouver la mesure de l'angle en ^B
dessin à main levée
au tableau derrière
SOH CAH TOA
(ici on cherche l'angle en B, on connaît le côté [BO] (Hyp) et le côté
[YO] Opposé à l'angle en ^B , donc on utilise la formule SOH)
Dans le triangle BOY est rectangle en Y, j'utilise la trigonométrie :
sin  B=YO
BO
(Opposé sur Hypoténuse)
on remplace par les valeurs connues
sin  B=4
5
=0,8
On a le sinus de l'angle ^B qui vaut 0,8, donc en
utilisant la touche
sin
1
de la calculatrice, on trouve
¿
B
≈
53
°
(arrondi au degré près ou à l'unité)
Exemple 2 Dans le triangle IJK rectangle en K, on a IK=7 m et JK=6
m, trouver la mesure de l'angle en J
( on cherche ^J, on connaît IK Opposé, on connait KJ Adjacent
on utilise TOA)
Dans le triangle IJK rectangle en K,
tan  J=IK
KJ
On remplace :
tan  J=7
6
≈1,167
Remarque : si on trouve une valeur approchée 3 décimales sont

nécessaires!
En tapant à la calculatrice
tan
1
1,167 ; on trouve
J
≈
49,4
°
Remarque : Si on avait pris 1,2 pour tan^J, on trouve J environ 50°
paragraphe IV Propriétés
Activité sur le tableur
Il semble d'après cette activité que ,
Formule 1:
tan x =
sin x
cos x
Attention
il n'est pas possible de diviser par 0!!! La formule ne sera valable
que pour les valeurs de x qui ne rendent pas nul cos(x)
Formule 2 : cosx
2
sin x
2
=1
En fait on écrit cos
2
x sin
2
x = 1
Démonstration :
schéma au tableau à reproduire
Je pars du membre de droite et je vais le transformer jusqu'à arriver
au membre de gauche
sinx
cosx=
AC
CB
AB
CB
=AC
CB ×CB AB =AC AB =tan xcqfd (Ce
Qu'il Fallait Démontrer )