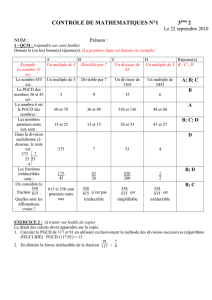
Exercice 5

1

2
► ►

3
▼

4
1) On va calculer le PGCD de 378 et 270 en utilisant l’algorithme d’Euclide.
Dividende
Diviseur
Reste
378
270
108
270
108
54
108
54
0
Pour compléter le tableau précédent, on a utilisé la touche de la calculatrice qui donne le
quotient et le reste de la division euclidienne demandée.
Autrement dit, 378 ( 1 + 270 6 108
Autrement dit, 270 ( 2 + 108 6 54
► ►

5
On en déduit que le PGCD de 378 et 270 est égal à 54 car il s’agit du dernier reste non nul obtenu en
effectuant les divisions euclidiennes successives.
On peut contrôler ce résultat en utilisant directement la touche de la calculatrice :
2)
:) Parmi les diviseurs communs à 378 et à 270, il s
L
agit de déterminer le plus grand possible car
le comité des fêtes veut faire le plus grand nombre de lots identiques en utilisant toutes les billes
et tous les calots. Ce problème revient donc à déterminer le PGCD de 378 et 270.
D’après la question précédente, on peut affirmer que ce comité des fêtes pourra faire 54 lots
identiques.
N) 378 T 54 ( 7 et 270 T 54 ( 5.