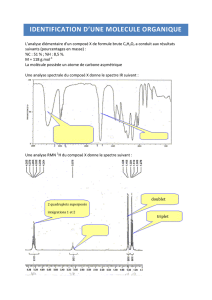
Physique quantique appliquée

Université Pierre et Marie Curie
M1 - OACOS & AP Année 2009–10
Physique quantique appliquée
TD n10: Niveaux de vibration-rotation des molécules diatomiques
On étudie, dans le référentiel du centre de masse, les états stationnaires d’un
système formé par deux atomes d’une molécule diatomique, système équivalent
à une particule …ctive de masse plongée dans le potentiel V(r).
On admet que le potentiel d’interaction V(r)entre les deux atomes ne dépend
que de leur distance ret a la forme présentée en …gure 1.
r
V(r)
1 - Donner les caractéristiques principales du potentiel V(r). On appellera
“re”la position d’équilibre.
2 - On montre que l’hamiltonien Hdu système est de la forme:
H=~2
21 r
@2
@r2rL2 r2~2+V(r)
Par analogie avec des expressions classiques de l’énergie, donner une inter-
prétation physique des di¤érents termes de l’hamiltonien: quels sont ceux qui
correspondent à une déformation de la molécule? et à une rotation?
3 - On montre (cf un TD précédent) que les trois opérateurs H,L2et Lz
commutent pour un tel potentiel. On en déduit alors que l’on peut chercher les
fonctions propres de Hsous la forme:
1

(r; ; ) = Rn;`(r)Ym
`(; )
où nest un nombre quantique dont on verra plus tard la signi…cation physique
et où Ym
`(; )sont les harmoniques sphériques. On note En;` l’énergie corre-
spondante.
Ecrire l’équation di¤érentielle radiale à laquelle satisfait la fonction Rn;`(r),
puis e¤ectuer le changement de fonction suivant:
un;`(r) = r Rn;`(r)
Ecrire la nouvelle équation di¤érentielle radiale obtenue, et montrer que cette
équation est équivalente à celle d’une particule à une dimension plongée dans
un potentiel e¤ectif Veff (r)que l’on déterminera.
4 - On cherche à déterminer l’expression des énergies En;` au voisinage de
la position d’équilibre re. Pour cela, on fait les approximations suivantes dans
l’équation di¤érentielle radiale:
on développe V(r)au voisinage du minimum reen se limitant au premier
terme en (rre)non nul. Le coe¢ cient de ce terme sera noté .
on remplace rpar redans le terme centrifuge provenant de l’énergie ciné-
tique de rotation.
a) Montrer que les approximations précédentes reviennent à écrire:
Veff (r) = V(re) + 1
2 !2(rre)2+`(`+ 1) ~B
Donner l’expression de Bet son unité.
b) Donner l’expression de !en fonction de et d2V(r)
dr2r=re
:
c) Ecrire l’équation radiale à laquelle satisfait un;`(r).
d) Montrer que cette équation est analogue à celle d’un oscillateur har-
monique de pulsation !et d’énergie E0
n;` que l’on dé…nira.
e) Que représente le nombre quantique net quelles valeurs peut-il prendre?
f) Donner les niveaux d’énergie En;` de la molécule en fonction de n,V0,!,
`et B.
g) Calculer Bet !pour la molécule HCl.
On donne:
= 1;6 1027 kg;re= 1;3Å; d2V(r)
dr2r=re
= 4;8 102Jm2
h) Donner l’allure du diagramme d’énergie pour les deux premiers niveaux
de vibration (n= 0 et n= 1) avec leur structure rotationnelle pour `= 0;1;2;et
3. Commenter.
i) Dans le cas d’un spectre de rotation pure (c’est-à-dire à n…xé), les règles
de sélection (Wigner-Eckart) impliquent que seules les transitions entre niveaux
d’énergie En;` et En;`1existent.
Donner l’expression des fréquences associées à ces transitions, puis montrer
que l’intervalle de fréquence entre 2 raies est constant et préciser sa valeur.
2

Application au spectre de Titan:
La …gure ci-dessous représente le spectre de Titan observé dans l’infrarouge
thermique par l’instrument Composite InfraRed Spectrometer (CIRS) à bord
de la sonde Cassini. Les émisions étroites superposées à l’émission continue
sont dues à des transitions entre niveaux d’énergie interne des molécules qui
composent l’atmosphère de Titan. La gamme de fréquence - ou d’énergie -
observée indique que ce sont des transitions de rotation pure ( 1cm1()
1;24:104eV () 3:1010 Hz).
Le paramètre Bde quelques molécules est donné dans le tableau ci-dessous.
Identi…er au moins 2 molécules présentes dans le spectre donné.
Molécule Bcm1
HCN 1.48
CO 1.93
N22.01
CH44.88
H260.8
Figure 1: Spectre de Titan observé par l’instrument Cassini/CIRS
3