circuits linéaires - mpsi1-fenelon-sainte

circuits linéaires
Table des matières
1 méthodes d’étude en régime permanent 2
1.1 Méthodologie générale . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 2
1.2 Premier exemple : circuit simple à sept éléments . . . . . . . . . . . . . . . 2
1.3 simplifications de la résolution . . . . . . . . . . . . . . . . . . . . . . . . . . 3
1.4 Théorème de superposition (ou th. d’Helmholtz) (Hors programme) . . . . . 3
1.5 Equivalence triangle-étoile - Théorème de Kennely (Hors programme) . . . . 4
1.6 ThéorèmedeMillman .............................. 5
1.7 utilisation des symétries . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 6
2 circuit RC série soumis à un échelon de tension 6
2.1 charge et décharge du condensateur . . . . . . . . . . . . . . . . . . . . . . . 7
2.1.1 casgénéral ................................ 7
2.1.2 mise en fonction de la source . . . . . . . . . . . . . . . . . . . . . . 7
2.1.3 extinction de la source (régime libre) . . . . . . . . . . . . . . . . . . 8
2.2 étudeénergétique................................. 8
3 circuit RL série soumis à un échelon de tension 9
3.1 évolution de l’intensité du courant électrique . . . . . . . . . . . . . . . . . . 9
3.1.1 casgénéral ................................ 9
3.1.2 établissement du courant . . . . . . . . . . . . . . . . . . . . . . . . . 9
3.1.3 extinction de la source (régime libre) . . . . . . . . . . . . . . . . . . 10
3.2 étudeénergétique................................. 11
4 circuit RLC série soumis à un échelon de tension 11
4.1 casgénéral..................................... 11
4.2 régime libre du circuit RLC série . . . . . . . . . . . . . . . . . . . . . . . . 12
4.2.1 régime pseudo-périodique . . . . . . . . . . . . . . . . . . . . . . . . 12
4.2.2 régimecritique .............................. 15
4.2.3 régime apériodique . . . . . . . . . . . . . . . . . . . . . . . . . . . . 15
4.3 mise sous tension du circuit RLC . . . . . . . . . . . . . . . . . . . . . . . . 16
1

Un circuit linéaire est un circuit constitué uniquement de composants linéaires c’est-à-dire
de composants pour lesquels tension et intensité sont reliées soit par une relation affine
soit par une équation différentielle linéaire à coefficients constants, du type
an
dnu
dtn+an−1
dn−1u
dtn−1+... +a1
du
dt +a0u+bn
dni
dtn+bn−1
dn−1i
dtn−1+... +b1
di
dt +b0i= 0
n est l’ordre du circuit. Nous étudierons les circuit d’ordre 1 et d’ordre 2.
On appelle :
- réponse libre ou régime libre d’un circuit, l’évolution de celui-ci en l’absence de tout gé-
nérateur.
- le régime du circuit est dit continu (ou stationnaire) lorsque toutes les grandeurs élec-
triques du circuit (intensités, tensions) sont indépendantes du temps.
-régime transitoire le régime s’établissant entre le moment où toutes les sources sont
éteintes et celui où le régime continu est établi.
1 méthodes d’étude en régime permanent
Connaissant les f.e.m. des générateurs et les composants du réseau, résoudre celui-ci c’est
déterminer l’intensité du courant qui circule dans chacune des branches.
1.1 Méthodologie générale
Pour effectuer la mise en équation puis la résolution d’un circuit électrique, on peut utiliser
la démarche suivante :
- dans un premier temps, numéroter les noeuds et les branches ;
- dans chaque branche du circuit, noter les courants (flèche pour le sens conventionnel et
nom) ;
- pour chaque élément, noter la tension à ses bornes (flèche et nom) ;
- mettre en équation en utilisant deux groupes de relations :
- un pour les aspects topologiques (organisation du réseau) : (n-1) lois des noeuds sont
nécessaires pour n noeuds recensés et (m-1) lois de mailles sont nécessaires pour m mailles
indépendantes recensées (une maille est indépendante si elle n’est pas une combinaison des
autres),
- un second pour les relations attachées à chaque élément utilisé.
- poser les hypothèses simplificatrices (courants ou tensions identiques, contraintes imposées
par les éléments, etc.) ;
- simplifier les relations en tenant compte des hypothèses — à ce stade on dispose d’un
système d’équations ;
- résoudre le système pour en extraire les grandeurs inconnues.
1.2 Premier exemple : circuit simple à sept éléments
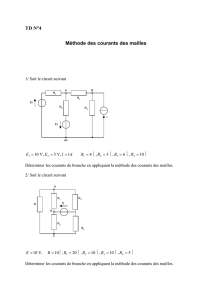
Dans le circuit, toutes les grandeurs électriques sont permanentes. Les éléments (résistances
et sources) sont complètement connus. On cherche à évaluer l’expression du courant I dans
la dernière résistance R.
2

- Identification des différentes grandeurs (tensions et courants)
- Courants : I1(t), I2(t), I3(t) et I(t) invariants, on peut donc écrire I1, I2, I3et I.
- Tensions : E1, E2, U, U1, U2, U3(notées sans la variable t car elles sont constantes).
- Identification de la topologie du réseau
- Quatre branches : celles de E1, E2, I3et U.
- Trois mailles indépendantes : (E1, R1, R), (E2, R2, R) et (I3, R3, R).
- Deux noeuds donc une seule loi des noeuds.
- Mise en équation
- 1 loi des noeuds : I1+ I2+ I3= I ;
- 3 lois des mailles : U = E1−R1I1; U = E2−R2I2; U = E3−R3I3(E3libre).
- U=RI
- Résolution : Le courant est exprimé dans chaque branche à l’aide des trois lois des
mailles puis son expression est intégrée dans la loi des noeuds :
I1=
−RI +E1
R1
I2=
−RI +E2
R2
−RI +E1
R1
+
−RI +E2
R2
+I3=I
(R1R2+R(R1+R2))I= (R2E1+R1E2+R1R2I3)
I=R2E1+R1E2+R1R2I3
R1R2+R(R1+R2)
- vérification de l’homogénéité
1.3 simplifications de la résolution
La résolution du réseau pécédent peut être simplifiée à l’aide de
- l’équivalence Thévenin-Norton : le circuit est équivalent à un générateur idéal de courant
d’intensité I3+E1
R1
+E2
R2
en parallèle avec la résistance R et une résistance R1R2
R1+R2
.
On remarquera que la résistance R3n’a aucun interêt dans le circuit.
- du pont diviseur de courant : I=1/R
1/R +R1+R2
R1R2
(I3+E1
R1
+E2
R2
).
On retrouve bien le résultat précédent.
exercices 7 bis - 11
1.4 Théorème de superposition (ou th. d’Helmholtz) (Hors programme)
Un circuit électrique ou électronique linéaire est régi par un système différentiel linéaire
à coefficients constants puisque ce circuit peut être modélisé par un réseau électrique
constitué uniquement de dipôles linéaires et que les lois de Kirchhoff se traduisent par
des équations linéaires. Les seconds membres de ces équations ne font intervenir que des
combinaisons linéaires et homogènes des forces électromotrices et des courants électromo-
teurs des sources idéales indépendantes de courant et de tension du réseau.
3

Dans un circuit électrique ou électronique linéaire comportant plusieurs sources
idéales indépendantes agissant simultanément, l’expression de la solution gé-
nérale donnant l’intensité du courant traversant une branche quelconque (ou
la tension à ses bornes) est égale à la somme algébrique des intensités des
courants traversant cette branche (ou des tensions à ses bornes) produits par
chacune des sources indépendantes agissant séparément, les autres sources in-
dépendantes étant "éteintes" et la configuration du réseau restant inchangée.
Autre énoncé : La "réponse" d’un réseau linéaire à une distribution de sources indépen-
dantes peut être considéré comme la superposition des réponses à chacune des sources, les
autres étant "éteintes".
Dans le cas précédent,
- si I3est éteinte, elle est équivalente à un interrupteur ouvert. Si E2est éteinte, elle
est équivalente à un fil. On a alors, avec l’équivalence Thévenin-Norton et le diviseur de
courant,
I/1all =1/R
1/R + 1/R1+ 1/R2
(E1/R1) = E1R2
R1R2+R(R1+R2)
- si E1est éteinte de même que I3, elle est équivalente à un fil. On a alors, en changeant
les indices 1 et 2 dans la relation précédente,
I/2all =1/R
1/R + 1/R1+ 1/R2
(E2/R2) = E2R1
R1R2+R(R1+R2)
- si E1et E2sont éteintes, elle sont équivalentes à des fils. On a alors, avec le diviseur de
courant,
I/3all =1/R
1/R + 1/R1+ 1/R2
I3=R2R1I3
R1R2+R(R1+R2)
La solution finale est I=I/1all +I/2all +I/3all
I=R2E1+R1E2+R1R2I3
R1R2+R(R1+R2)
1.5 Equivalence triangle-étoile - Théorème de Kennely (Hors programme)
On cherche les conditions sur les résistances afin que les deux montages ci-dessus soient
équivalents. Les relations de passage du triangle vers l’étoile sont :
rA=RABRAC
RAB +RAC +RBC
4

et les autres par permutations circulaires.
exemple :
On considère le circuit représenté sur la figure ci-dessus. L’objectif est de calculer la valeur
du courant I et du courant I1.
Il est difficile de résoudre rapidement ce problème. On peeut transformer le traingle ABC
en étoile, chacune des résistances de l’étoile valant 100.100
100 + 100 + 100 = 33,3Ω. On obtient
alors le circuit suivant :
On calcule la résistance équivalente au circuit : Req = 33,33 + (233,33.133,33/(233.33 +
133.33) = 118,17Ω.
I = E
Req
=84,6 mA . Ensuite on calcule V =7,17 V . Et on en déduit : I1=V
133,33
=53,87 mA
exercice 9
1.6 Théorème de Millman
Ce théorème permet la détermination directe de potentiel de noeud d’un réseau de résis-
tances par rapport à un potentiel de référence, à partir de la loi des noeuds.
On considère un noeud A auquel aboutissent k branches ; les potentiels Vides extrémités
5