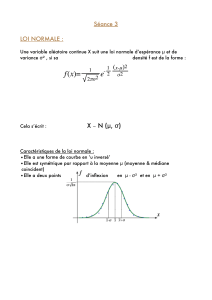
Variables aléatoires à densité I Intégrales généralisées à bornes

fRa
fR
f
FRF(x) = Zx
a
f(t)t
Z+∞
a
f(t)t
F+∞.
Z+∞
a
f(t)t=
F−∞ Za
−∞
f(t)t
Za
−∞
f(t)t= lim
x−→−∞ Za
x
f(t)dt
F+∞ −∞
Z+∞
−∞
f(t)t=
fRf(t) = (0 si t < 1
1
t2si t>1
xZ0
x
exp(t) dt=

(Ω,T, P )
f:R−→ R R
fR∀t∈R,
fR
Z+∞
−∞
f(t)tZ+∞
−∞
f(t)t=
f(t) = 
0t < 1
1
t2t>1
X: Ω −→ R
f:R−→ R
f X

F X f
X
Flim
x→−∞
F(x) =
FR
FC1R
F x
F0(x) =
fR
X: Ω −→ RF.
FR
FC1R
X
f f(x) = F0(x)x F

X
RC1
X F
X f
f(t) = 
0t < 0
e−tt>0
Y=X3
X f. c d
c<d
P(X > c) = 1 −P(X6c) =
P(c < X 6d) = Zd
c
f(t)dt
P(X=c) =
P(c < X < d) = P(c6X6d) =

[c6X6d]
f
x=c x =d
f]−∞, a[
a∈Rx
F(x) = P(X6x) = Zx
−∞
f(t)t=
si x>a
0 si x<a
X f
Z+∞
−∞
t f(t)t
X
E(X) = Z+∞
−∞
fRf(t) = (cos t t ∈h0,π
2i
0
f X
X