Test : principe fondamental de la dynamique et aspect énergétique

Test : principe fondamental de la dynamique et aspect énergétique
Durée : 45 minutes
Objectifs
•Projection de forces.
•Calcul de durée d'accélération / décélération ou d'accélération / décélération ou de vitesse en fin de phase
d'accélération / décélération à partir d'un profil de vitesse ou du principe fondamental de la dynamique.
•Relation entre les vitesses linéaires et angulaires.
•Utilisation de la relation donnant le moment d'une force à partir de son module et du rayon d'action.
•Couples moteurs et résistants.
•Calcul de travaux de forces, travaux moteurs et résistants.
•Bilan énergétique : énergies absorbée, utiles, pertes et rendement.
•Théorème de l'énergie cinétique.
Dans tous les exemples donnés ci-dessous, l'accélération de la pesanteur sera prise égale à 9,81 m.s-2.
Premier exemple d'énoncé
On considère un système de levage dont le schéma de principe de la partie mécanique est représenté
ci-dessous. Le solide est accroché à un câble passant dans la gorge d'une poulie et enroulé autour d'un
tambour. Le mât sur lequel est fixée la poulie n'est pas représenté.
L'objectif de cette partie est de déterminer les caractéristiques mécaniques, couple utile et vitesse de rotation,
de la machine à courant continu.
1. Force de traction sur le câble
Le déplacement de la charge se fait uniquement selon l'axe vertical, la composante de la vitesse selon cette
direction est notée v et comptée positive lorsque la charge monte.
a. Placer sur le schéma le poids du solide et la force de traction
T
qui lui est appliquée par
l'intermédiaire du câble.
b. Écrire l'équation traduisant la loi fondamentale de la dynamique pour les systèmes en translation.
Test principe fondamental de la dynamique
et aspect énergétique 1 TS2 ET 2014-2015

c. Projeter cette équation sur l'axe vertical, orienté vers le haut, et en déduire une relation entre le module
T de la force de traction, la masse m, l'accélération de la pesanteur g et v.
d. Calculer T pour les deux situations suivantes avec une masse du solide égale à xx kg :
•La charge monte à vitesse constante.
•La charge monte avec une accélération de xx m.s-2.
2. Bilan énergétique
a. Calculer les travaux de la force
T
et du poids lors d'une montée de xx m à vitesse constante.
Préciser si ces travaux sont moteur ou résistant.
b. Lors d'une phase d'accélération, le module de la force
⃗
T
est égal à xx N et le poids est inchangé.
Les travaux de ces deux forces ne sont plus égaux en valeur absolue, à quoi correspond la différence ?
3. Vitesse de rotation du tambour
Le tambour est l'organe sur lequel s'enroule le câble lors de la montée de la charge. Son rayon est noté Rt et
est égal à xx cm.
a. Calculer le périmètre du tambour.
b. Combien de tours doit faire le tambour pour que la charge monte de xx m ? (ou de combien monte la
charge si le tambour fait xx tours ?)
c. Calculer la vitesse de rotation du tambour si la charge monte à la vitesse linéaire de xx m/s. (ou calculer
la vitesse de montée de la charge si la vitesse de rotation du tambour est égale à xx tr/min)
4. Moment du couple sur l'arbre du tambour
a. En supposant que la force appliquée sur le solide a le même module que la force appliquée au niveau
du tambour, exprimer le moment du couple sur l'arbre du tambour en fonction de T et de Rt puis calculer
sa valeur pour T = xx N.
b. Déduire de la question précédente la puissance sur l'arbre du tambour si la vitesse de rotation est égale
à xx tr/min.
Les pertes n'étant pas négligeables en pratique, la puissance sur l'arbre du tambour est égale à xx W.
5. Vitesse de rotation et couple sur l'arbre du moteur
Les valeurs du couple et de la vitesse de rotation trouvées précédemment ne correspondent pas à un moteur à
courant continu, il est nécessaire d'insérer un réducteur entre les arbres du tambour et du moteur. Ce
réducteur présente un rapport de réduction égal à xx et un rendement de xx %.
a. Après avoir précisé quelle puissance est mise en jeu sur l'arbre relié au tambour et quelle puissance est
mise en jeu sur l'arbre du moteur, calculer la puissance utile sur l'arbre du moteur.
b. Calculer la vitesse de rotation du moteur lorsque celle du tambour est égale à xx tr/min puis en déduire
le couple utile sur l'arbre du moteur.
Remarque : le texte xx signifie qu'il s'agit de valeurs numériques susceptibles de changer...
Test principe fondamental de la dynamique
et aspect énergétique 2 TS2 ET 2014-2015

Deuxième exemple d'énoncé
Le schéma ci-contre représente un ascenseur
constitué d'une cabine de masse notée M et d'un
contrepoids de masse notée Mc. Les deux éléments
sont reliés par câble et mus par un treuil entraîné par
un moto-réducteur. La poulie du treuil a un diamètre
noté DT.
1. Mise en équation
a. Représenter le poids de la cabine et le poids du
contrepoids sur le schéma en précisant le nom
de leur point d'application.
b. Établir les expressions des moments des
couples des poids de la cabine, noté
Ccab
, et
du contrepoids, noté
Ccntp
par rapport à l'axe
de rotation du treuil.
c. Si La cabine est en montée, ces couples sont-ils
moteurs ou résistants ?
d. Calculer la vitesse angulaire de la poulie du
treuil si la cabine monte à xx m/s.
Le couple imposé par le moto-réducteur est noté
Cmot
et le moment d'inertie équivalent sur l'arbre du
treuil est noté Jeq
e. Écrire la relation traduisant le principe fondamental de la dynamique pour les systèmes en rotation.
2. Calculs du couple pour le moto-réducteur
a. Déterminer le couple sur l'arbre du moto-réducteur pour que la vitesse de déplacement soit égale à xx
m/s.
b. Déterminer le couple sur l'arbre du moto-réducteur pour que la vitesse de déplacement passe de 0 m/s
(arrêt) à xx m/s en xx s si Jeq = xx kg.m2.
3. Bilan énergétique pour un fonctionnement en montée
a. Calculer les travaux du poids et du contrepoids pour un déplacement de xx m et en déduire l'énergie
fournie par le moto-réducteur.
b. Le rendement du système de motorisation est égal à xx %, déterminer les puissances électriques
nécessaires au déplacement de la question précédente pour une vitesse constante de xx m/s puis yy m/s.
c. Lors d'une phase d'accélération, la somme des travaux des poids de la cabine et du contrepoids sont
plus faibles en valeur absolue que l'énergie fournie par le moto-réducteur , à quoi correspond la
différence ?
Remarque : le texte xx signifie qu'il s'agit de valeurs numériques susceptibles de changer...
Test principe fondamental de la dynamique
et aspect énergétique 3 TS2 ET 2014-2015

Troisième exemple d'énoncé
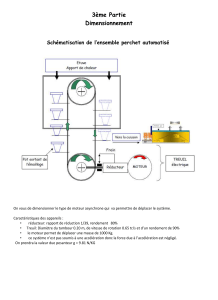
Le schéma ci-dessous représente un véhicule utilitaire électrique. L'objectif est de déterminer les
caractéristiques mécaniques, couple utile et vitesse de rotation, de la machine à courant continu utilisée pour
sa motorisation.
Le véhicule a une masse en charge (poids à vide et charge utile) de 1700 kg et sa vitesse est de 25 km/h.
La figure ci-contre est une représentation
schématique du véhicule lors d'un déplacement vers
la droite.
La force
R1
représentée sur la roue de droite,
motrice, se décompose en une composante normale,
résistance à l'enfoncement, et une composante
tangentielle qui est la force de traction.
La force
R2
représentée sur la roue de gauche,
non motrice, se décompose en une composante
normale, résistance à l'enfoncement, et une
composante tangentielle qui est la force de résistance
à l'avancement.
La composante de la vitesse dans la direction du
déplacement est notée v.
1. Force de traction
a. Placer sur le graphe les composantes normales et tangentielles des forces
R1
et
R2
. Faire
apparaître le poids en précisant le nom de son point d'application.
b. Écrire l'équation traduisant la loi fondamentale de la dynamique pour les systèmes en translation.
c. Projeter cette équation sur l'axe vertical, orienté vers le haut, et en déduire une relation entre les
composantes normales de
R1
et
R2
, la masse m du véhicule et l'accélération de la pesanteur g.
d. Projeter cette même équation sur l'axe
horizontal, orienté vers la droite, et en déduire
une relation entre les composantes tangentielles
de
R1
et
R2
, la masse m et v.
La force de résistance à l'avancement, composante
tangentielle de
R2
, est calculée par la relation
R2t=m g
avec µ = 0,015.
e. Calculer R2t puis en déduire la composante
tangentielle de
R1
, notée R1t, lorsque la
vitesse est constante puis lorsque l'accélération
est égale à 0,4 m.s-2.
Variante : le véhicule monte une rampe faisant un
angle a avec l'horizontale (voir le schéma ci-contre).
2. Moment du couple sur un arbre de roue
Le diamètre Droue d'une roue est égal à xx cm.
a. Exprimer la vitesse angulaire de rotation de l'arbre de roue, notée Wroue, en fonction de Droue et de la
vitesse d'avancement du véhicule. Calculer Wroue pour une vitesse de xx km/h.
Test principe fondamental de la dynamique
et aspect énergétique 4 TS2 ET 2014-2015

b. Exprimer le moment Croue de la composante tangentielle de
R1
en fonction de R1t et de Droue.
c. Lorsque le véhicule se déplace à xx km/h sur le plat, R1t = xx N, calculer Croue.
3. Moment du couple sur l'arbre moteur
Le couple sur l'arbre moteur est transmis à la roue par l'intermédiaire d'un réducteur tel que
Ωm
Ωroue
=xx
avec Wm la vitesse angulaire de rotation de l'arbre moteur ; le rendement du réducteur est égal à xx %.
a. Calculer la vitesse angulaire de rotation du moteur si le véhicule roule à xx km/h.
b. Exprimer la puissance Proue sur l'arbre de la roue en fonction de Croue et Wroue et celle, notée Pm, sur
l'arbre du moteur en fonction de Cm et Wm (Wm est la vitesse angulaire de l'arbre du moteur).
c. À partir de la relation entre Proue, Pm et le rendement du réducteur, déterminer l'expression de Cm en
fonction de Croue, Wroue, Wm et du rendement du réducteur.
d. Calculer Cm lorsque le déplacement a lieu à vitesse constante et égale à xx km/h sur le plat et en
déduire la puissance utile du moteur pour ce fonctionnement.
4. Moment d'inertie équivalent sur l'arbre du moteur
L'objectif de cette question est de déterminer le moment d'inertie équivalent Jeq sur l'arbre du moteur. Chaque
roue, il y en a quatre, a un moment d'inertie Jroue = xx kg.m2, celui du moteur Jm = xx kg.m2.
a. Exprimer les énergies cinétiques :
•du véhicule en fonction de sa masse et de sa vitesse.
•d'une roue en fonction de son moment d'inertie et de sa vitesse angulaire de rotation.
•du moteur en fonction de son moment d'inertie et de sa vitesse angulaire de rotation.
b. Rappeler les relations entre v et Wroue puis entre Wroue et Wm. En déduire l'expression de l'énergie
cinétique totale EcT en fonction de m, Jroue, Jm, Droue et Wm.
Remarque : le texte xx signifie qu'il s'agit de valeurs numériques susceptibles de changer...
Test principe fondamental de la dynamique
et aspect énergétique 5 TS2 ET 2014-2015