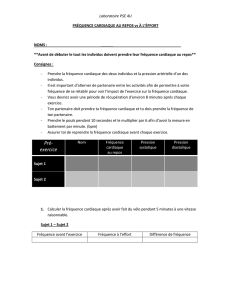
114: Anneau des séries formelles. Applications.

(an)A
APanXnA[[X]]
A A[[X]] : a7→ (a, 0,0, . . .)
v(S) = inf {i|ai6= 0}+∞
(ai) (bi)
iPi
k=0 akbi−k
(A[[X]],+,∗)
v(x+y)>min(v(x), v(y))
v(x∗y)>v(a)+(b)A
A[[X]]
v(x)>v(y)u x =uy
K K[[X]] K−
a06= 0 A[[X]]
K[[X]] Xi
K[[X]]
A A[X]
A[[X]]
A A[[X]]
A[[X]] A

d(x, y)=0 x=y e−v(x−y)
d(S, T )>0d(S, T ) = 0 ⇔S=T D(S, T ) = D(T, S)D(R, T )6
sup(D(R, S), D(S, T )) 6D(R, S) + D(S, T )
d
K[[x]]
K[x]
K[x]K[[x]] d K[[x]] (K[x], d)
(a1,...an,0, . . .)
Si=Pan,iXn
n an,i PSi=PnPian,iXn
0
SiS∗(PSi)
S T sitit0= 0
tn,j XnTi
PsiTi
S◦T
S◦T=Pk>0Pk
i=0 aibkiXkb0,0= 1 bk,0= 0 T= 0 S◦T=a0
S=XnS◦T=TnT=X S◦T=S S = 1 S◦T= 1
(PiSi)◦T=P(Si◦T) (S∗T)◦U=
(S∗U)◦(T∗U)
1
X
S=PanXnS0= (n+ 1)an+1Xn
s7→ s0d
(ST )0=S0T+T S0(S◦T)0=T0(S0 ◦ T)Sn0=nS0∗Sn−1
(1 −X)−10= (1 −x)−2
exp(X) = PXn/n! (1 + X)α
Log(1 + x) = P(−1n−1Xn/n
exp((a+b)X=exp(aX)exp(bX)exp(aX)0=aexp(aX)log(1 + X)0= (1 +
X)−1exp(log(1 + X)) = 1 + X log(1 + exp(X)−1)) = X

(1 + X)α=PCn
αXnCn α= (α). . . (α−k)/k!
exp(Mn(C)) = Gln(C)
X(exp(zX)−1)−1=PBn(z)/n!XnBn
z
Bk(X) = Nk−1PN−1
a=0 Bk((X+a)/N)Bk(X) = Xk−1/2.k.Xk−1+
An
P∞
n=0 AnXnP∞ n=0 An/n!Xn
PCk
nDk=n!
PDk/k!Xk1
e−z/(1 −z)Dkk!/e + 1/2
Dkk!/e
Bnn
Bn+1 =Pn
k=0 Ck
nBkPbn/n!Xn
T0=eXT Bn=Pn
1S(n, k)
Cn−1
2n−2/n
A
APanXn
r||A|| < r
||A|| > r anrnr
1/r =limsup|an|1/n
a0

a(n)+l1a(n−1) +. . . +ln−2a= 0
ai
t2y00 + (a+ 1)ty0+ (t2+ 1/4)y= 0 tαϕ(t)
ϕ[(α+
n)(α+n−2) + (a+ 1)(α+n)+1/4]un+un−2= 0 ϕ(0) = 1
u2n= 1/(QP(α+ 2k)P=X(X−1) + (a+ 1)X+ 1/4) u2n+1 = 0
0+
Qn
k=1(1−Xk)
n→ ∞ Pp(n)Xnp(n)
n
1/[(1 −X)(1 −X2)(1 −X5)]