Un angle est une portion de plan qui est délimitée par deux demi

Chapitre : Angles
I) Notion d’angle
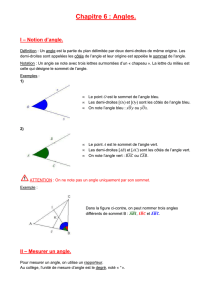
Définition: Un angle est une portion de plan qui est délimitée par deux
demi-droites de même origine.
Les deux demi-droites sont appelées côtés de l’angle, alors
que leur origine commune est appelée sommet de l’angle.
Exemple : _ Le point O est le sommet de l’angle.
_ Les demi-droites [OA) et [OB) sont les côtés de l’angle.
Notation : _ Un angle se note généralement à l’aide de trois lettres.
_ La lettre au centre, surmontée d’un « chapeau », est celle qui
désigne le sommet de l’angle.
Exemple : Cet angle peut être désigné par différentes écritures :
_ On peut l’appeler 
 ou encore   À chaque fois, la lettre O désigne le sommet de l’angle.
_ On peut également l’appeler 
 ou  .
II) Mesure d’un angle
1) Unité : le degré
Définition : Un angle plat peut-être partagé en 180 parties égales.
Un degré (noté 1°) est la mesure de chacune de ces parties.
Notation : Lorsque la mesure d’un angle 
 est égale à 40°, on note
.
Remarques : _ Un angle plat mesure 180° (180 fois 1°).
_ Pour mesurer un angle, on utilise un rapporteur.
_ La plupart des rapporteurs possèdent une double graduation,
qui va de 0 à 180 degrés.
Cette double graduation est sources de nombreuses erreurs…
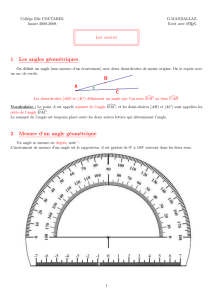
2) Mesurer un angle
Méthode : Pour déterminer la mesure en degrés de l’angle 
 :
• On commence par placer le centre du rapporteur sur le sommet de l’angle (ici le point A).
• On fait pivoter le rapporteur autour de son centre de façon à ce que l’un des côtés de l’angle passe par une
des deux graduations "0" (intérieure ou extérieure), et que l’autre côté de l’angle passe sous une autre graduation
du rapporteur.
• En faisant bien attention à ne pas se tromper de graduation, compter le nombre de graduations à partir du
zéro pour arriver jusqu’au deuxième côté de l’angle.

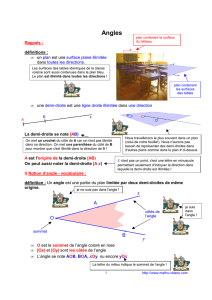
3) Construire un angle
Méthode : Pour tracer un angle 
mesurant 75° (en supposant que le segment [AB] est déjà tracé) :
• On commence par placer le centre du rapporteur sur le point qui sera le sommet de l’angle (ici le point A).
• Si besoin est, on prolonge le segment [AB] en la demi-droite [AB).
• On fait pivoter le rapporteur autour de son centre de façon à ce que la demi-droite [AB) passe par une des
deux graduations "0" (intérieure ou extérieure).
• En faisant bien attention à ne pas se tromper de graduation, compter le nombre de graduations à partir du
zéro pour arriver jusqu’à la mesure demandée (ici 75°), et faire une marque au crayon.
• Oter le rapporteur et tracer le deuxième côté de l’angle.
4) Angles particuliers
On peut classer les angles selon leur mesure    
 :
Propriété : Soient A, B et C trois points distincts deux à deux ;
_ Dire que "les droites (AB) et (AC) sont perpendiculaires" revient à dire que "l’angle 
 est un angle droit".
_ Dire que "les points A, B et C sont alignés" revient à dire que "l’angle 
est soit nul, soit plat".
Définition : _ On dira de deux angles qu’ils sont adjacents s’ils ont le même sommet, un côté en commun, et qu’ils sont situés de part
et d’autre de ce côté commun.
_ On dira de deux angles qu’ils sont complémentaires s’ils sont adjacents et si la somme de leurs mesures est égale à 90◦.
_ On dira de deux angles qu’ils sont supplémentaires s’ils sont adjacents et si la somme de leurs mesures est égale à 180°.
Exemple :

III) Bissectrice d’un angle
Définition: La bissectrice d’un angle est la demi-droite qui a pour origine le sommet de l’angle, et qui partage l’angle en deux
angles adjacents de même mesure.
Exemple :
Méthode : Construire la bissectrice d’un angle
On mesure l’angle à l’aide du rapporteur ; puis on divise cette mesure par 2, et on trace l’angle moitié.