cours : les angles

CHAPITRE 5
COURS :LES ANGLES
1 Qu’est-ce qu’un angle ?
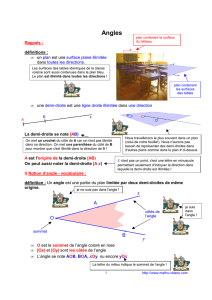
Définition :
Un angle est une portion de plan délimitée par deux demi-droites ayant la même origine.
Les deux demi-droites sont appelées côtés de l’angle, alors que leur origine commune est appelée
sommet de l’angle.
Illustration :
x
y
α
Côtés de l’angle
Sommet de l’angle
O
B
A
Cet angle peut être désigné par différentes écritures :
ÏOn peut l’appeler α(lettre de l’alphabet grec, qui se prononce "alpha", équivalent de notre "a").
ÏOn peut l’appeler AOB ou encore BOA (il faut seulement que la lettre désignant le sommet de
l’angle soit placée au milieu).
ÏOn peut également l’appeler xO y ou yOx.
2 Mesure d’un angle
Définition :
On peut mesurer l’"ouverture" d’un angle ; l’unité de mesure que l’on utilise au collège est le degré.
L’instrument qui nous servira à mesurer des angles s’appelle un rapporteur.
Voici un rapporteur, gradué en degrés ; ce rappor-
teur a une double graduation, qui va de 0 à 180
degrés. BAttention ! ! Cette double graduation est
source de nombreuses erreurs...
0
180
10
170
20
160
30
150
40
140
50
130
60
120
70
110
80
100
90
90
100
80
110
70
120
60
130
50
140
40
150
30
160
20
170
10
180
0
6ème Page 1/4 Cours Angles

Comment mesurer un angle à l’aide du rapporteur ?
0
180
10
170
20
160
30
150
40
140
50
130
60
120
70
110
80
100
90
90
100
80
110
70
120
60
130
50
140
40
150
30
160
20
170
10
180
0
A
B
C
180
0
170
10
160
20
150
30
140
40
130
50
120
60
110
70
100
80
90
90
80
100
70
110
60
120
50
130
40
140
30
150
20
160
10
170
0
180
A
B
C
B AC =60◦ B AC =109◦
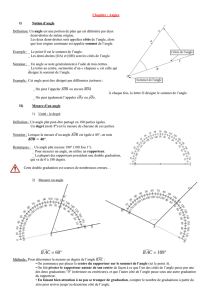
Pour déterminer la mesure en degrés de l’angle B AC :
•On commence par placer le centre du rapporteur sur le sommet de l’angle (ici le point A).
•On fait pivoter le rapporteur autour de son centre de façon à ce que l’un des côtés de l’angle
passe par une des deux graduations "0" (intérieure ou extérieure), et que l’autre côté de
l’angle passe sous une autre graduation du rapporteur.
•En faisant bien attention à ne pas se tromper de graduation, compter le nombre de gradua-
tions à partir du zéro pour arriver jusqu’au deuxième côté de l’angle.
Comment tracer un angle de mesure donnée à l’aide d’un rapporteur ?
0
180
10
170
20
160
30
150
40
140
50
130
60
120
70
110
80
100
90
90
100
80
110
70
120
60
130
50
140
40
150
30
160
20
170
10
180
0
A B
A B
75◦
Pour tracer un angle B AC mesurant 75◦(en supposant que le segment [AB]est déjà tracé) :
•On commence par placer le centre du rapporteur sur le point qui sera le sommet de l’angle
(ici le point A).
•Si besoin est, on prolonge le segment [AB] en la demi-droite [AB].
•On fait pivoter le rapporteur autour de son centre de façon à ce que la demi-droite [AB]
passe par une des deux graduations "0" (intérieure ou extérieure).
•En faisant bien attention à ne pas se tromper de graduation, compter le nombre de gradua-
tions à partir du zéro pour arriver jusqu’à la mesure demandée (ici 75◦), et faire une marque
au crayon.
•Oter le rapporteur et tracer le deuxième côté de l’angle.
6ème Page 2/4 Cours Angles

3 Différents types d’angles
On peut classer les angles selon leur mesure α= B AC :
α=0◦0◦<α<90◦α=90◦90◦<α<180◦α=180◦
Angle nul Angle aigu Angle droit Angle obtus Angle plat
ACB
A
C
B
A
C
B
A
C
B
A
CB
Propriétés :
Soient A,Bet Ctrois points distincts deux à deux ;
ÏDire que "les droites (AB) et (AC ) sont perpendiculaires" revient à dire que "l’angle B AC est un
angle droit".
ÏDire que "les points A,Bet Csont alignés" revient à dire que "l’angle B AC est soit nul, soit plat".
Définitions :
ÏOn dira de deux angles qu’ils sont adjacents s’ils ont le même sommet, un côté en commun, et
qu’ils sont situés de part et d’autre de ce côté commun.
ÏOn dira de deux angles qu’ils sont complémentaires si la somme de leurs mesures est égale à 90◦.
ÏOn dira de deux angles qu’ils sont supplémentaires si la somme de leurs mesures est égale à 180◦.
AB
C
D
A
B
C
D
B AD et D AC sont adjacents et complémentaires. B AD et D AC sont adjacents et supplémentaires.
4 Bissectrice d’un angle
Définition :
La bissectrice d’un angle est la demi-droite qui a pour origine le sommet de l’angle, et qui partage
l’angle en deux angles de même mesure.
A
B
C
bissectrice de
d
BAC
6ème Page 3/4 Cours Angles

Comment tracer la bissectrice d’un angle donné
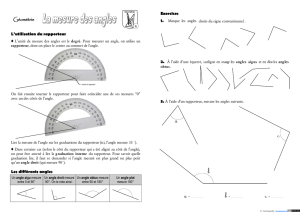
Avec un rapporteur :
On mesure l’angle à l’aide du rapporteur ; puis on divise cette mesure par 2, et on trace l’angle
moitié.
0
180
10
170
20
160
30
150
40
140
50
130
60
120
70
110
80
100
90
90
100
80
110
70
120
60
130
50
140
40
150
30
160
20
170
10
180
0
A
B
C
A
B
C
Avec un compas :
On trace deux arcs de cercle de centre A, de même rayon, venant couper les deux côtés de l’angle
aux points Iet J; puis, en prenant pour centres ces deux points, on trace à nouveau deux arcs de
même rayon que les arcs précédents, se croisant en un point D. La bissectrice de l’angle B AC est
la demi-droite [AD).
A
B
C
I
J
A
B
C
I
J
D
A
B
C
I
J
D
6ème Page 4/4 Cours Angles