Chapitre 7 : Angles

Chapitre 7 : Angles
Ils sont utilisés dans les coordonnées GPS, en construction (toit d’une
maison, pente d’une route), dans les boussoles, en astronomie, …
1) Rappels, définitions :
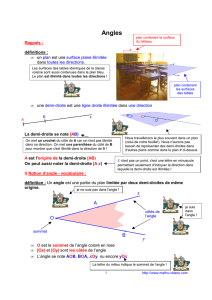
Un angle est formé par deux demi-droites qui ont la même origine.
On trace un arc de cercle entre les deux demi-droites.
Rappel : sur une demi-droite, les points (A, B, C,…) s’écrivent à côté d’un petit
trait en prolongeant. Les directions (x, y , …) s’écrivent au bord sans trait.
y O est le sommet de l’angle.
C [Ox) et [Oy) sont les côtés de l’angle.
Ils peuvent aussi se noter [OA) et [OC).
On peut noter le même angle de plusieurs
O A B x manières :
O = xOy = AOC = BOC = …
(Le sommet O est toujours au milieu)

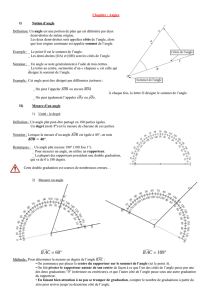
2) Mesure d’un angle :
Remarques :
● On compte toujours à partir de zéro pour ne pas confondre les deux
graduations et on vérifie que la mesure obtenue correspond bien à l’angle (plus
petit ou plus grand que l’angle droit qui fait 90°).
● On peut toujours prolonger les demi-droites pour qu’elles dépassent du
rapporteur.
y
x
Pour mesurer l’angle xOy , on place le centre du rapporteur sur le sommet O
de l’angle et on aligne le zéro de la graduation sur un côté.
On lit alors la mesure de l’angle sur l’autre côté.
xOy = 30° ( et pas 150° !)
Les angles se mesurent en degrés, noté °. Le tour complet fait 360°.
L’angle droit mesure 90° (un quart de tour).
Pour mesurer un angle, on utilise un rapporteur qui est un demi-cercle partagé
en 180 parties égales. Il y a souvent deux graduations.

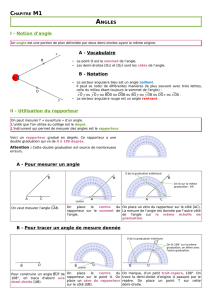
3) Construire un angle :
Remarques :
● Attention encore à ne pas confondre 30° et 150° qui sont en face.
● Pour reproduire un angle avec le compas, on choisit un point sur chaque
demi-droite et on reproduit le triangle formé par ces deux points et le
sommet de l’angle.
Pour construire un angle xOy de 30°, on commence par tracer une demi-droite
[Ox).
Puis on pose le centre du rapporteur sur le point O en alignant le zéro de la
graduation sur la demi-droite.
x
On repère la graduation 30° à partir de zéro et on trace un point en face de
cette graduation.
On enlève le rapporteur et on trace la demi-droite d’origine O passant par
ce point. On trace l’arc de cercle et on note sa mesure juste à côté.

4) Quand les droites sont parallèles :
Angles alternes-internes :
Ils sont situés de chaque côté de la
droite (), et « entre » les droites ( d )
et ( d’ ).
Propriétés :
(d’’)
(d)
(d’)
Si deux angles alternes-internes sont définis par deux droites parallèles alors
ils ont la même mesure.
Si deux angles alternes-internes ont la même mesure alors ils sont définis par
deux droites parallèles.
Cas particulier : les angles sont droits.
On retrouve la propriété :
Si deux droites sont perpendiculaires à une même droite, alors elles sont
parallèles.

Annexe : extrait du programme officiel 2016 :
- Caractérisation angulaire du parallélisme, angles alternes / internes.
Mettre en œuvre ou écrire un protocole de construction d'une figure géométrique.
Les problèmes de construction constituent un champ privilégié de l'activité géométrique tout au long du
cycle 4. Ces problèmes, diversifiés dans leur nature et la connexion qu'ils entretiennent avec différents
champs mathématiques, scientifiques, technologiques ou artistiques, sont abordés avec les instruments de
tracé et de mesure. Dans la continuité du cycle 3, les élèves se familiarisent avec les fonctionnalités d'un
logiciel de géométrie dynamique ou de programmation pour construire des figures.