Enoncé et corrigé pdf

Pondichéry 2013. Enseignement spécifique
EXERCICE 4 (6 points) (commun à tous les candidats)
Dans une entreprise, on s’intéresse à la probabilité qu’un salarié soit absent durant une période d’épidémie
de grippe.
•Un salarié malade est absent
•La première semaine de travail, le salarié n’est pas malade.
•Si la semaine nle salarié n’est pas malade, il tombe malade la semaine n+1avec une probabilité égale
à0, 04.
•Si la semaine nle salarié est malade, il reste malade la semaine n+1avec une probabilité égale à 0, 24.
On désigne, pour tout entier naturel nsupérieur ou égal à 1,parEnl’événement « le salarié est absent pour cause
de maladie la n-ième semaine ». On note pnla probabilité de l’événement En.
On a ainsi : p1=0et, pour tout entier naturel nsupérieur ou égal à 1:0!pn<1.
1) a) Déterminer la valeur de p3,àl’aided’unarbredeprobabilité.
b) Sachant que le salarié a été absent pour cause de maladie la troisième semaine, déterminer la probabilité
qu’il ait été aussi absent pour cause de maladie la deuxième semaine.
2) a) Recopier sur la copie et compléter l’arbre de probabilité donné ci-dessous
En
En
pn
...
...
...
...
...
En+1
En+1
En+1
En+1
b) Montrer que, pour tout entier naturel nsupérieur ou égal à 1,pn+1=0, 2pn+0, 04.
c) Montrer que la suite (un)définie pour tout entier naturel nsupérieur ou égal à 1par un=pn—0, 05
est une suite géométrique dont on donnera le premier terme et la raison r.Endéduirel’expressiondeun
puis de pnen fonction de net r.
d) En déduire la limite de la suite (pn).
e) On admet dans cette question que la suite (pn)est croissante. On considère l’algorithme suivant :
Vari abl es Ket Jsont des entiers naturels, Pest un nombre réel
Initialisation Pprend la valeur 0
Jprend la valeur 1
Entrée Saisir la valeur de K
Traite ment Tant que P<0,05−10−K
Pprend la valeur 0, 2 ×P+0, 04
Jprend la valeur J+1
Fin tant que
Sortie Afficher J
Aquoicorrespondl’affichagefinalJ?
Pourquoi est-on sûr que cet algorithme s’arrête ?
3) Cette entreprise emploie 220 salariés. Pour la suite on admet que la probabilité pour qu’unsalariésoitmalade
une semaine donnée durant cette période d’épidémie est égaleàp=0, 05.
On suppose que l’état de santé d’un salarié ne dépend pas de l’état de santé de ses collègues.
On désigne par Xla variable aléatoire qui donne le nombre de salariés maladesunesemainedonnée.
a) Justifier que la variable aléatoire Xsuit une loi binomiale dont on donnera les paramètres.
http ://www.maths-france.fr 1 c ⃝Jean-Louis Rouget, 2014. Tous droits réservés.

Calculer l’espérance mathématique µet l’écart type σde la variable aléatoire X.
b) On admet que l’on peut approcher la loi de la variable aléatoire X−µ
σpar la loi normale centrée réduite
c’est-à-dire de paramètres 0et 1.
On note Zune variable aléatoire suivant la loi normale centrée réduite. Le tableau suivant donne les
probabilités de l’événement Z<xpour quelques valeurs du nombre réel x.
x−1, 55 −1, 24 −0, 93 −0, 62 −0, 31 0, 00 0, 31 0, 62 0, 93 1, 24 1, 55
P(Z<x)0, 061 0, 108 0, 177 0, 268 0, 379 0, 500 0, 621 0, 732 0, 823 0, 892 0, 939
Calculer, au moyen de l’approximation proposée en question b), une valeur approchée à 10−2près de la
probabilité de l’événement : « le nombre de salariés absents dans l’entreprise au cours d’une semaine donnée
est supérieur ou égal à 7et inférieur ou égal à 15 ».
http ://www.maths-france.fr 2 c ⃝Jean-Louis Rouget, 2014. Tous droits réservés.

Pondichéry 2013. Enseignement spécifique
EXERCICE 4 : corrigé
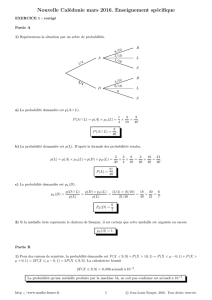
1) a) Représentons la situation par un arbre (E1est impossible et donc E1est certain).
E2
E2
0, 04
0, 96
0, 24
0, 76
0, 96
0, 04
E3
E3
E3
E3
E1
La probabilité demandée est p3=p(E3).Laformuledesprobabilitéstotalesfournit
p3=p(E2∩E3)+p!E2∩E3"=p(E2)×pE2(E3)+p!E2"×pE2(E3)
=0, 04 ×0, 24 +0, 96 ×0, 04 =0, 0096 +0, 0384 =0, 048.
p3=0, 048.
b) La probabilité demandée est pE3(E2).
pE3(E2)=p(E2∩E3)
p(E3)=p(E2)×pE2(E3) p(E3)=0, 04 ×0, 24 0, 048 =0, 0096 0, 048 =96 480 =1 5=0, 2.
pE3(E2)=0, 2.
2) a)
En
En
pn
1−pn
0, 24
0, 76
0, 96
0, 04
En+1
En+1
En+1
En+1
b) Soit nun entier naturel supérieur ou égal à 1.D’aprèslaformuledesprobabilitéstotales.
pn+1=p(En)×pEn(En+1)+p!En"×pEn(En+1)=0, 24pn+0, 04(1−pn)
=0, 2pn+0, 04.
Pour tout nsupérieur ou égal à 1,pn+1=0, 2pn+0, 04.
http ://www.maths-france.fr 1 c ⃝Jean-Louis Rouget, 2014. Tous droits réservés.

c) Soit nun entier naturel supérieur ou égal à 1.
un+1=pn+1—0, 05 =0, 2pn+0, 04 −0, 05 =0, 2pn−0, 01 =0, 2(pn−0, 05)=0, 2un.
Donc la suite (un)est une suite géométrique de raison r=0, 2 et de premier terme u1=p1−0, 05 =−0, 05.
On sait alors que pour tout entier naturel non nul n,
un=u1×rn−1=−0, 05 ×0, 2n−1,
et donc
pn=un+0, 05 =0, 05 −0, 05 ×0, 2n−1.
pour tout nsupérieur ou égal à 1,pn=0, 05 −0, 05 ×0, 2n−1.
d) Puisque −1<0,2<1,onsaitque lim
n→+∞
0, 2n−1=0.Onendéduitque
lim
n→+∞
pn=0, 05.
e) Al’étape1,Pcontient p1et plus généralement, à l’étape j!1,Pcontient pj.L’algorithmes’arrêtedèsquela
variable Jcontient un numéro jtel que pj!0, 05 −10−k(où kest la valeur entrée dans la variable K). A partir de ce
numéro, tous les termes de la suite sont supérieurs ou égaux à 0, 05 −10−k.
L’algorithme affiche donc le plus petit numéro jtel que pj!0, 05 −10−k.
Puisque la suite (pn)converge vers 0, 05,pourtoutentiernaturelK,ilexisteunrangn0tel que pour n!n0,
pn!0, 05 −10−K.Onendéduitquecetalgorithmes’arrête.
3) a) Xsuit une loi binomiale. En effet,
•220 expériences identiques et indépendantes sont effectuées ;
•chaque expérience a deux issues à savoir « le salarié est malade » avec une probabilité p=0, 05 et « le salarié
n’est pas malade » avec une probabilité p=1−0, 05 =0, 95.
Donc, Xsuit une loi binomiale de paramètres n=220 et p=0, 05.
On sait que µ=np =220 ×0, 05 =11 et σ=#np(1−p)=√10, 45 =3, 23 à10−2près.
b) La probabilité demandée est p(7"X"15).Or,
7"X"15 ⇔7−µ
σ"X−µ σ"15 −µ σ.
La probabilité demandée est donc aussi p$7−11
√10, 45 "X−µ
σ"15 −11
√10, 45 %ou encore p$−1, 24 "X−µ
σ"1, 24%en
arrondissant les bornes de l’encadrement à 10−2.
L’énoncé nous dit que cette probabilité est environ :
p(−1, 24 "Z"1, 24)=p(Z"1, 24)−p(Z"−1, 24)=p(Z<1,24)−p(Z<−1, 24)
=0, 892 −0, 108 =0, 784.
La probabilité demandée vaut environ 0, 784.
http ://www.maths-france.fr 2 c ⃝Jean-Louis Rouget, 2014. Tous droits réservés.