Corrigé - Site Personnel de Arnaud de Saint Julien

1
©Arnaud de Saint Julien - MPSI Lycée La Merci 2016-2017
Corrigé du DM n°9 pour le mercredi 7/03
Groupes d’ordre quatre
1
Obligatoire
Exercice 1 (un modèle géométrique du groupe de Klein) On munit le plan d’un repère orthonormé, d et d′ sont l’axe des abscisses et l’axe des ordonnées. On note sd et sd′ les symétries
orthogonales par rapport à d et d′ . On note G = {id, sd , sd′ , − id}.
1. Soit M un point du plan de coordonnées (x, y). On a
sd ◦ s′d (x, y) = sd (sd′ (x, y)) = sd (−x, y) = (−x, −y) = − id(x, y).
Ainsi sd ◦ s′d = id, la symétrie de centre (0, 0).
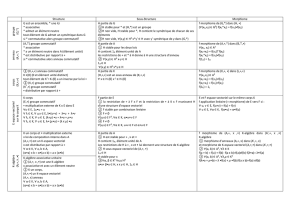
2. Démontrer que (G, ◦) est un groupe commutatif. De même, on montre par exemple que
sd ◦ −id = sd′ . On résume tous les calculs de «produits» (composés ici) dans G dans le
tableau suivant :
◦
id
sd
sd′
− id
id
id
sd
sd′
− id
sd
sd
id
− id
sd′
sd′
sd′
− id
id
sd
− id
− id
sd′ .
sd
id
Cela montre que G est stable pour la loi ◦. On remarque aussi que les quatre éléments de G
sont inversibles et égaux à leur inverse, car ∀g ∈ G, on a g ◦ g = id.
Ainsi, G est un sous-groupe du groupe des bijections de R2 car :
• il contient l’identité
• il est stable par composition et passage à l’inverse
Il est de plus commutatif.
3. Est-il isomorphe qui lui aussi possède 4 éléments ? On pourra calculer les carrés de chaque
élément.
Nous allons montrer que G n’est pas isomorphe au groupe des racines quatrièmes de l’unité.
La raison est que dans G, tous les éléments élevés au carré donnent l’identité, tandis que
dans U4 , on a par exemple i2 = −1 qui n’est pas égal à 1. Détaillons.
Supposons qu’il existe un isomorphisme φ : U4 → G. On a alors φ(i) ∈ G, donc φ(i)◦φ(i) = id.
Mais φ(1) = id, car le morphisme φ transforme le neutre 1 de U4 en le neutre de G, c’est-àdire id. D’autre part, comme φ est un morphisme, on a φ(i) ◦ φ(i) = φ(i × i) = φ(i2 ) = φ(−1).
On a donc φ(1) = φ(−1) et donc 1 = −1 car φ est injective. Contradiction.
Exercice 2 Soit G = {1, a, b, c} un groupe multiplicatif à 4 éléments. On note 1 son élément
neutre. On suppose que ∀x ∈ G, x2 = 1. On sait alors d’après un exercice que G est commutatif.
1. Soit x ∈ G. Comme x × x = 1, x est l’inverse de x.
2. Que valent les produits ab, ac et bc ?
Comme G est un groupe, il est stable par produit, donc ab ∈ G. Si ab = 1, on a alors aussi
ba = 1 (car G est commutatif) et alors b est l’inverse de a, mais alors b = a (par unicité de
l’inverse) ce qui est faux. Donc ab 6= 1.
Supposons que ab = a. Alors en multipliant par l’inverse de a (par la gauche), on aurait
b = 1, ce qui est faux. Donc ab 6= a.
De même si ab = b, en mutipliant par l’inverse de b (à droite), on obtient a = 1, ce qui est
faux, donc ab 6= b.
On a donc ab = c. On montre la même façon que :
ab = c,
ac =,
bc = a.
2
©Arnaud de Saint Julien - MPSI Lycée La Merci 2016-2017
3. On note K le groupe de Klein vu ci-dessus. On définit une application f de G sur K en posant
f (1) = id, f (a) = sd , f (b) = sd′ et f (c) = − id. Cette application est même une bijection de
G sur K.
On f (ab) = f (c) = − id = sd ◦ sd′ = f (a) ◦ f (b).
De même, f (ac) = f (b) = sd′ = sd ◦ − id = f (a) ◦ f (c). On montre de la même façon que
pour tout x et y de G, on a f (xy) = f (x) ◦ f (y). Cela prouve que f est un morphisme, et
comme f est bijective, c’est un isomorphisme de G sur K.
2
Facultatif
Exercice 3 (Un théorème de Lagrange) Soit (G, ×) un groupe commutatif de cardinal n.
1. Soit g ∈ G. Démontrer que l’application f : G → G définie par f (x) = gx est une bijection.
Soit y ∈ G. On a y = f (x) ⇐⇒ y = gx ⇐⇒ g −1 y = x. L’application f est donc bijective.
Y
2. En déduire que g n = e en calculant de deux façons différentes le produit
gx.
D’une part,
Y
gx =
x∈G
D’autre part,
Y
x∈G
Y
Y
x∈G
g × xn =
Y
g
x∈G
gx =
Y
x∈G
n
Y
x=
x∈G
f (x) =
Y
x∈G
g×x .
x∈G
Y
n
y=
y∈G
Y
g car f est une bijection de G dans G. Ainsi
x∈G
g d’où x = e.
x∈G
3. En déduire les sous-groupes finis de C∗ .
Soit G un sous-groupe fini de C ∗ de cardinal n. Alors d’après le théorème de Lagrange, pour
tout z dans G, on a z n = 1, autrement dit z ∈ Un . Ainsi G ⊂ Un . Réciproquement, pour
tout n ∈ N∗ , Un est bien un sous-groupe fini de C∗ .
Exercice 4 (Groupe cyclique d’ordre 4) Soit (G, ×) un groupe de cardinal 4. On sait d’après
le théorème de Lagrange (exercice 3) que ∀x ∈ G, x4 = 1. On appelle ordre de x le plus petit
entier k ∈ N∗ tel que xk = 1.
1. Soit x ∈ G différent de 1. On note p son ordre. Démontrer que p ∈ {2, 4}.
Comme x4 = 1, on a p 6 4. Si p = 3, alors x3 = 1 et donc en multipliant par x, on obtient
x4 = x, d’où 1 = x, ce qui est faux. Enfin p 6= 1 car sinon x = 1, donc p ∈ {2, 4}.
2. Que dire du groupe G si tout élément de G différent de 1 est d’ordre deux ? Dans ce cas,
d’après l’exercice 2, G est isomorphe au groupe de Klein K.
3. On suppose qu’il existe x ∈ G d’ordre 4.
(a) Justifier que les éléments 1, x, x2 , x3 de G sont 2 à 2 distincts.
Déjà x 6= 1, x2 6= 1 et x3 6= 1 car sinon l’ordre de x ne serait pas égal à 4.
Si x = x2 , alors en multipliant par x−1 , on obtient 1 = x, ce qui est faux. De même si
x = x3 , on a 1 = x2 , faux. Enfin, si x2 = x3 , en multipliant par l’inverse de x2 , on a
1 = x, faux.
Ainsi G qui possède 4 éléments contient l’ensemble {1, x, x2 , x3 } lui aussi à 4 éléments.
Onen déduit que G = {1, x, x2 , x3 }.
(b) En déduire que G est isomorphe à U4 . On considère l’application f : G → U4 définie
par f (1) = 1, f (x) = i, f (x2 ) = −1 et f (x3 ) = −i.
L’application f est par construction une bijection de G sur U4 . Reste à vérifier que c’est
un morphisme.
Remarquons que −1 = i2 et −i = i3 . On a donc par récurrence immédiate que pour
tout k ∈ N, f (xk ) = ik . On a donc pour tout k et n dans N :
f (xk × xn ) = f (xk+n ) = ik+n = ik × in = f (xk ) × f (xn ).
Ceci montre que f est un morphisme.
Nous avons donc achever la classification des groupes d’ordre quatre : à isomorphisme près,
ils sont de deux types : soit isomorphe au groupe de Klein, soit isomorphe au groupe des racines
4-ièmes de l’unité.