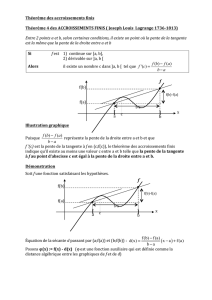
1.8 Le théorème des accroissements finis

1. Applications différentiables: Le théorème des accroissements finis 33
1.8 Le théorème des accroissements finis
Rappelons le résultat classique pour les fonctions d’une variable réelle à valeurs
dans R.
1.8.1 THÉORÈME (THÉORÈME DES ACCROISSEMENTS FINIS SUR R)
Soit fune fonction continue sur un intervalle [a,b], à valeurs dans R, dérivable sur
]a,b[.
Alors, il existe c2]a,b[tel que
f(b)f(a)= f0(c)(ba).
(où il existe q2]0, 1[tel que
f(b)f(a)= f0(a+q(ba))(ba).
Une autre version ( plus faible) de ce résultat est l’inégalité des accroissements finis :
1.8.2 THÉORÈME (L’INÉGALITÉ DES ACCROISSEMENTS FINIS )
Soit fune fonction continue sur un intervalle [a,b], à valeurs dans R, dérivable sur
]a,b[. Soit M0 telle que |f0(x)|M, pour tout x2[a,b], alors |f(y)f(x)|
M|yx|pour tout x,y2[a,b].
On en déduit une première extension du théorème des accroissements finis pour
les fonctions définies sur un ouvert d’un espace vectoriel normé Eà valeurs dans R.
1.8.3 DÉFINITION
1) Soit Eun espace vectoriel, a,b2E. Le segment [a,b]est le sous-ensemble de E
défini par
[a,b]={x2E; il existe t2[0, 1]tel que x=a+t(ba)}
2) Un sous-ensemble U⇢Eest dit convexe si pour tout a,b2Ule segment
[a,b]⇢U.
1.8.4 THÉORÈME (THÉORÈME DES ACCROISSEMENTS FINIS À VALEURS DANS R)
Soit f:U!Rune fonction différentiable dans l’ouvert U⇢E. Soit a,b2U, si le
segment [a,b]est contenu dans U, il existe q2]0, 1[telle que
f(b)f(a)=Df(a+q(ba)).(ba)
ce qui est équivalent à dire qu’il existe c2]a,b[tel que f(b)f(a)=Df(c).(ba).

1. Applications différentiables: Le théorème des accroissements finis 34
FIGURE 1.1 – convexe
FIGURE 1.2 – non convexe
Démonstration: On applique le théorème des accroissements finis à la fonction g:
[0, 1]!R,t7! g(t)= f(a+t(ba)). Alors, g=fAoù A:[0, 1]!Rnest
l’application définie par A(t)=a+t(ba).
gest différentiable sur [0, 1], comme composée de fonctions différentiables et
g0(t)=Df(A(t))(DA(t)) = Df(a+t(ba)).(ba)
Il existe donc q2]0, 1[tel que g(1)g(0)=g0(q),
qui se traduit par : il existe q2]0, 1[tel que
f(b)f(a)=Df(a+q(ba)).(ba).
1.8.6 REMARQUE.L’exemple suivant montre que ce résultat est faux si fest à valeurs
dans un espace vectoriel de dimension 2.
1.8.7 EXEMPLE.Soit f:R!R2,x7! f(x)=(x2,x3). Sa différentielle au point xest
Df(x)=(2x,3x2). D’autre part, f(1)f(0)=(1, 1)et pour tout c2R,Df(c)=
(2c,3c2)6=(1, 1)on montre ainsi, le théorème précédent ne s’applique pas à f.
On a néanmoins, le corollaire suivant : si on n’impose pas aux différentielles des
composantes de fsoient évaluées en un même point c:
1.8.8 COROLLAIRE
Soit f:U!Rm,x7! (f1(x),...,fm(x)) une fonction différentiable. Soit a,b2U,
si le segment [a,b]est contenu dans U, il existe mpoints c1,...,cm2]a,b[telle que
pour tout j2{1, . . . , m}on a
fj(b)fj(a)=Df(cj).(ba)

1. Applications différentiables: Le théorème des accroissements finis 35
Démonstration: On applique 1.8.4 à chaque composante fjde f.
Une autre variante du théorème des accroissement finis où l’égalité est rempla-
cée par une inégalité sur les normes.
1.8.10 THÉORÈME (L’INÉGALITÉ DES ACCROISSEMENTS FINIS)
Soit f:U!Rmune application différentiable. Uouvert de Rn.
Pour tout a,b2Rntels que le segment [a,b]⇢U,ona:
kf(b)f(a)k sup
x2]a,b[kDf(x)k!.kbak
Démonstration: On suppose f(b)f(a)6=0, sinon l’inégalité est évidente. On pose
v=f(b)f(a)
kf(b)f(a)k. On considére la forme linéaire continue y, définie par : pour tout
y2F,y(y)=<y,v>où <., . >est le produit scalaire standard sur Rm.
D’après 1.8.4, il existe q2]0, 1[telle que y(f(b)f(a))=y(f(b))y(f(a))=
Dyf(a+q(ba)).(ba)=yDf(a+qy(ba))(ba)s’écrit aussi
<f(b)f(a),v>=<Df(a+q(ba))(ba),v>ou encore
kf(b)f(a)k=<Df(a+q(ba))(ba),v>
et une application de l’inégalité de Cauchy-Schwarz nous donne :
|<Df(a+q(ba))(ba),v>|kDf(a+q(ba))(ba)kkvkkDf(a+q(ba))(ba)k
d’où kf(b)f(a)kkDf(a+q(ba))(ba)kkDf(a+q(ba))kk(ba)k,
finalement kf(b)f(a)k⇣supx2]a,b[kDf(x)k⌘.k(ba)k⌅
1.8.12 LEMME
Soit g:[0, 1]!Fune application différentiable telle que il existe M0 tel que,
pour tout t2]0, 1[on ait kDg(t)kM. Alors kg(1)g(0)kM.
Démonstration: Soit e>0 fixé.
on pose Se={t2[0, 1]|8s2[0, t],kg(s)g(0)k(M+e).s}. Comme Seest
une partie non vide et bornée de R, elle admet une borne supérieure, qu’on notera
t0.
On veut montrer que t0=1.
Si t0<1, alors par définition de la borne supérieure, il existe une suite hn>0
telle que lim
n!+•hn=0 et kg(t0+hn)g(0)k>(M+e).(t0+hn). D’où par conti-
nuité de get passage à la limite, on aura kg(t0)g(0)k(M+e).t0. Alors
kg(t0+hn)g(t0)kkg(t0+hn)g(0)kkg(t0)g(0)k>(M+e).(t0+hn)(M+e).t0=
(M+e).hnainsi kg(t0+hn)g(t0)
hnk>M+eet par passage à la limite on obtient
kDg(t0)kM+e>M, ceci contredit l’hypothèse kDg(t)kMpour tout t2
[0, 1]. Donc t0=1. Par suite, pour tout e>0, kg(1)g(0)k(M+e)ce qui
signifie kg(1)g(0)kM.

1. Applications différentiables: Le théorème des accroissements finis 36
1.8.14 THÉORÈME (L’INÉGALITÉ DES ACCROISSEMENTS FINIS (CAS GÉNÉRAL))
Soient Eet Fdeux evn et f:U!Fune application différentiable. Uouvert de E.
Soient x,y2Utels que le segment [x,y]⇢U. On suppose qu’il existe M0
telle que kDf(x+t(yx))kMpour tout t2]0, 1[, alors
kf(y)f(x)kMkxyk(1.3)
Démonstration: Soient x,y2Utels que le segment [x,y]⇢U. On définit g:[0, 1]!F,
t7! g(t)= f(x+t(yx)). Alors, pour tout t2[0, 1], on aura Dg(t)=Df(x+t(yx)).(yx)
et par suite kDg(t)kkDf(x+t(yx))k.kyxkM.kyxk.
On applique le lemme précédent à gpour obtenir le résultat
kf(y)f(x)k=kg(1)g(0)kMkyxk
1.8.1 Quelques applications du théorème des accroissements finis
1.8.16 COROLLAIRE
Soient Eet Fdeux evn. f:U!Fune application différentiable. Uouvert de E.
Soit T2L(E,F). Pour tout a,b2Etels que le segment [a,b]⇢U,ona:
kf(b)f(a)T(ba)kkbak sup
x2]a,b[kDf(x)Tk!. (1.4)
En particulier, si T=Df(a)on aura
kf(b)f(a)Df(a)(ba)kkbak sup
x2]a,b[kDf(x)Df(a)k!. (1.5)
Démonstration: Résulte de l’inégalité des accroissement finis appliquée à fTet de
la linéarité de Tqui entraîne DT(x)=T.⌅
Soient E=E1⇥...⇥Enet Fdes espaces vectoriels normés , U⇢Eun ouvert et
f:U!Fune application.
On a vu précédemment que si fest différentiable en tout point a2U, alors
Df(a)=(D1f(a),...,Dnf(a)) et chaque composante Dif(a)2L(E,F), mais que la
réciproque est en générale fausse.
Le résultat suivant donne le lien entre continuité des dérivées partielles et conti-
nuité de la différentielle.

1. Applications différentiables: Le théorème des accroissements finis 37
1.8.18 THÉORÈME
Soient E=E1⇥...⇥Enet Fdes espaces vectoriels normés , U⇢Eun ouvert et
f:U!Fune application.
Alors fest de classe C1si et seulement si pour tout j2{1, . . . , n},Djfexiste et
est continue.
Démonstration: ”=)” Si Df est continue il en est de même de ses composantes Dif,
donc les dérivées partielles sont continues.
”(=” Supposons que pour tout j2{1, . . . , n},Djfexiste et est continue.
Pour alléger les notatiosn on prendra n=2, la même technique marche pour
n3.
Soit a=(a1,a2)2Uet (h1,h2)2E=E1⇥E2, on écrit
f(a+h)f(a)= f(a1+h1,a2+h2)f(a1,a2)
=f(a1+h1,a2+h2)f(a1+h1,a2)+ f(a1+h1,a2)f(a1,a2)
Soit #>0. Par hypothèse, il existe d>0 tel que pour kh1k<det kh2k<don a
kD1f(a1+h1,a2+h2)D1f(a1,a2)k<#et kD2f(a1+h1,a2+h2)D2f(a1,a2)k<#.
D’après le corollaire 1.8.16, on a
kf(a1+h1,a2+h2)f(a1+h1,a2)D2f(a1,a2)h2k
kh2ksup
s2]a2,a2+h2[kD2f(a1+h1,s)D2f(a1,a2)k.
et
kf(a1+h1,a2)f(a1,a2)D1f(a1,a2)h1k
kh1ksup
t2]a1,a1+h1[kD1f(t,a2)D1f(a1,a2)k.
D’où
kf(a+h)f(a)(D1f(a),D2f(a)) ⇣h1
h2⌘k#(kh1k+kh1k)
Ainsi fest différentiable et de différentielle Df(a)=(D1f(a),D2f(a)), comme D1f
et D2fsont continues, il en est de même de Df.⌅
1.8.20 DÉFINITION (APPLICATION LIPSCHITZIENNE)
Soient Eet Fdeux espaces vectoriels normés et K0.
Une application f:U!Fest dite K-lipschitzienne (ou lipschitzienne de rapport
K) si pour tout x,y2Uon a
kf(x)f(y)kKkxyk.