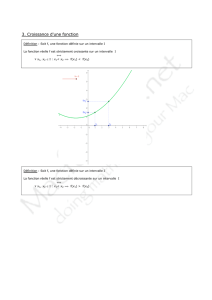
Déterminer les images par la fonction carré des nombres suivants :

fonction carré

Déterminer les carrés des nombres suivants :
•8
•–6
•0,5
•–1,5
•𝟑
•64
•36
•0,25
•2,25
•3

Déterminer les carrés des nombres suivants :
•𝟑
𝟒
•−𝟏
𝟐
•𝟏𝟎−𝟑
•𝟏𝟎 𝟔
•𝟐𝟏𝟎
•𝟗
𝟏𝟔
•𝟏
𝟒
•𝟏𝟎−𝟔
•𝟏𝟎 𝟏𝟐
•𝟐𝟐𝟎

Compléter :
•81 est le carré de ………………………
•Le carré de 𝟑est …………………
•………………. est le carré de 1,5
•………….… est le carré de –𝟔
•9
•3
•2,25
•6

VRAI ou FAUX :
•7 est solution de (x–3) ² = 16
•–3 est solution de x² + 9 = 0
•𝟐
𝟐est solution de 2 x ² –1 = 0
•Si b = 2 a, alors b ² = 4 a ²
•Si b = 2 a, alors b ² = 2 a ²
•Si b = 2 a, alors b ² = 4 a
•VRAI
•FAUX
•VRAI
•VRAI
•FAUX sauf si a = 0
•FAUX sauf si a = 0 ou a = 0,5