Télécharger

PROFESSEURS ASSOCIÉS – 1 bis rue Alexandre Dumas – 78100 Saint-Germain-en-Laye - Tél [phone]
Fiche  FONCTIONS DE REFERENCE 
FONCTIONS ASSOCIEES 1S
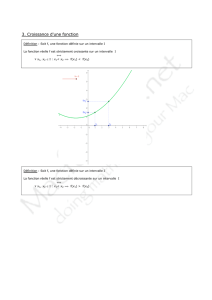
TECHNIQUE 1  DEFINITION DE FONCTIONS AFFINES :
Définition : Les fonctions affines sont les fonctions de la forme
()f x ax b
, où a et b sont deux réels quelconques.
 Le coefficient a est appelé coefficient directeur.
 Le coefficient b est appelé ordonnée à l'origine.
Propriétés, Variations : Pour toute fonction affine de type
()f x ax b
, les variations dépendent du signe du coefficient directeur
a :
 Si
0a
, la fonction est strictement croissante sur 4.
 Si
0a
, la fonction est strictement décroissante sur 4.
 Si
0a
, la fonction est constante sur 4.
Tableau de variations d'une fonction affine :
Si a>0
Si a<0
Remarques :
 Parfois, il faut bien réduire l'expression pour reconnaître la forme
()f x ax b
.
 Le coefficient directeur peut être présent dans le 2ème terme comme
dans
( ) 4 3f x x
: le coefficient directeur est 3.
TECHNIQUE 2  FONCTION CARRE :
Définition : La fonction carré est la fonction est définie sur 4 et qui à
tout réel x, associe le réel
( ) ²f x x
.
Courbe représentative : La courbe de la fonction carré est une
parabole.
La courbe est symétrique par rapport à l'axe des ordonnées.
Variations de la fonction carré :
 Sur l'intervalle ];0], la fonction carré est strictement
décroissante.
 Sur l'intervalle [0;+[, la fonction carré est strictement croissante.
Tableau de variations de la fonction carré :
On remarquera que la fonction carré admet un minimum qui vaut 0, en
x=0.
Conséquence sur la comparaison de carrés :
Pour comparer deux nombres au carré, il faut :
 Que les deux nombres soient de même signe.
 Connaître la comparaison des deux nombres.
 Utiliser alors la propriété des variations de la fonction carré.
1. Si a<b0,
2. et comme la fonction carré
est strictement décroissante
sur ];0],
3. alors a²>b²0².
1. Si 0a<b,
2. et comme la fonction carré
est strictement croissante sur
[0;+[,
3. alors 0²a²<b².
Remarques :
 Si dans les données, on part de x², c'est que l'on a des propriétés en
ordonnées et que donc on recherche des abscisses x.
 Si dans les données, on part de x (et simplement de x), c'est que l'on
parle d'abscisses et que donc on recherche des ordonnées x².
TECHNIQUE 3  FONCTION CUBE :
Définition : La fonction cube est la fonction qui est définie sur 4 et qui
à tout réel x, associe le réel
3
()f x x
.
Courbe représentative : La courbe de la fonction cube est de la forme.
La courbe est symétrique par rapport à l'origine du repère O.
Variations de la fonction cube :
 Sur 4, la fonction cube est strictement croissante.
Tableau de variations de la fonction cube :
On remarquera que la courbe passe par l'origine O du repère.
Conséquence sur la comparaison de cubes :
Pour comparer deux nombres au cube, il faut :
 Connaître la comparaison des deux nombres.
 Utiliser alors la propriété des variations de la fonction cube.
 Il n'y a pas de condition de signe comme la fonction carré.
1. Si a<b,
2. et comme la fonction cube est strictement croissante sur 4,
3. alors a3<b3.
Equations de cubes : On admettra :
33
a b a b  
.
Remarques :
 Si dans les données, on part de x3, c'est que l'on a des propriétés en
ordonnées et que donc on recherche des abscisses x.
 Si dans les données, on part de x (et simplement de x), c'est que l'on
parle d'abscisses et que donc on recherche des ordonnées x3.
TECHNIQUE 4 − FONCTION INVERSE :
Définition : La fonction inverse est la fonction qui est définie sur 4* et
qui à tout réel x non nul, associe le réel
1
()fx x
.
Courbe représentative : La courbe de la fonction inverse est
l'hyperbole.
La courbe est symétrique par rapport à l'origine du repère O.
Variations de la fonction inverse :
 Sur]−;0[, la fonction inverse est strictement décroissante.
 Sur ]0;+[, la fonction inverse est strictement décroissante.
Tableau de variations de la fonction inverse :
Conséquence sur la comparaison d'inverses :
Pour comparer des inverses de deux nombres, il faut :
 Que les deux nombres soient de même signe et non nul.
 Connaître la comparaison des deux nombres.
 Utiliser alors la propriété des variations de la fonction inverse.

PROFESSEURS ASSOCIÉS – 1 bis rue Alexandre Dumas – 78100 Saint-Germain-en-Laye - Tél [phone]
1. Si a<b<0,
2. et comme la fonction
inverse est strictement
décroissante sur ];0[,
3. alors
11
ab
.
1. Si 0<a<b,
2. et comme la fonction inverse
est strictement décroissante
sur ]0;+[,
3. alors
11
ab
.
Remarques :
 Si dans les données, on part de
1
x
, c'est que l'on a des propriétés en
ordonnées et que donc on recherche des abscisses x.
 Si dans les données, on part de x (et simplement de x), c'est que l'on
parle d'abscisses et que donc on recherche des ordonnées
1
x
.
TECHNIQUE 5 − FONCTION RACINE CARRE :
Définition : La fonction racine carré est la fonction qui est définie sur
[0;+[ et qui à tout réel x positif ou nul, associe le réel
()f x x
.
Courbe représentative : La courbe de la fonction racine carré est la
suivante :
Variations de la fonction racine carré :
 Sur [0;+[, la fonction racine carré est strictement croissante.
Tableau de variations de la fonction racine carrée :
On remarquera que la fonction racine carrée admet un minimum qui vaut
0, en x=0.
Conséquence sur la comparaison de racines carrés :
Pour comparer deux racines carrées, il faut :
 Que les deux nombres soient positifs ou nuls.
 Connaître la comparaison des deux nombres.
 Utiliser alors la propriété des variations de la fonction racine carré.
1. Si 0a<b,
2. et comme la fonction racine carré est strictement croissante sur
[0;+[,
3. alors
0ab
.
Remarques :
 Si dans les données, on part de
x
, c'est que l'on a des propriétés
en ordonnées et que donc on recherche des abscisses x.
 Si dans les données, on part de x (et simplement de x), c'est que l'on
parle d'abscisses et que donc on recherche des ordonnées
x
.
TECHNIQUE 6  FONCTION VALEUR ABSOLUE :
Définition : La fonction absolue est la fonction définie sur 4 et qui à
tout réel x de 4, associe le réel
()f x x
.
Propriété de simplification :
 Pour tout réel x0,
xx
.
 Pour tout réel x0,
xx
.
Variations de la fonction valeur absolue :
 Sur l'intervalle ];0], la fonction valeur absolue est strictement
décroissante.
 Sur l'intervalle [0;+[, la fonction valeur absolue est strictement
croissante.
Tableau de variations de la fonction valeur absolue :
On remarquera que la fonction valeur absolue admet un minimum qui
vaut 0, en x=0.
Conséquence sur la comparaison de valeurs absolues :
Pour comparer des inverses de deux nombres, il faut :
 Que les deux nombres soient de même signe.
 Connaître la comparaison des deux nombres.
 Utiliser alors la propriété des variations de la fonction valeur
absolue.
1. Si a<b0,
2. et comme la fonction valeur
absolue est strictement
décroissante sur ];0],
3. alors
0ab
.
1. Si 0a<b,
2. et comme la fonction valeur
absolue est strictement
croissante sur [0;+[,
3. alors
0ab
.
TECHNIQUE 6  COMPARAISON D'IMAGES :
But : il s'agit de comparer les images f(a) et f(b).
Méthode :
1. Il faut d'abord comparer les antécédents a et b.
2. Il faut ensuite connaître les variations de la fonction affine f.
3. On applique ensuite les propriétés suivantes :
 Si
ab
ET f est strictement croissante sur un intervalle
contenant a et b, alors
( ) ( )f a f b
.
 Si
ab
ET f est strictement décroissante sur un intervalle
contenant a et b, alors
( ) ( )f a f b
.
 Si
ab
ET f est constante sur un intervalle contenant a et b,
alors
( ) ( )f a f b
.
Remarques :
 Les fonctions f seront les fonctions de référence : il faudra alors se
souvenir des variations de ces fonctions-là.
 Il faut commencer par comparer les antécédents, et à l'aide des
variations des fonctions de référence, on peut comparer les images.
Exemples :
 Si f est strictement croissante et comme
2 1 2 3
, alors
(2 1) (2 3)ff
.
 Si f est strictement décroissante et comme
2 5 1 2 3 1  
, alors
(2 5 1) (2 3 3)ff  
.
Technique 10  Croissances comparées :
Idée : il s'agit ici de comparer les images d'un même nombre mais avec
des fonctions différentes.
Propriété :
Soient les fonctions
:
11
()fx x
;
3
2()f x x
;
2
3()f x x
;
4()f x x
;
5()f x x
De courbe
respective C1 ; C2,
C3, C4 et C5.

PROFESSEURS ASSOCIÉS – 1 bis rue Alexandre Dumas – 78100 Saint-Germain-en-Laye - Tél [phone]
Graphiquement, on observe que :
 Sur ]0;1[,
32 1
x x x x x
.
 Sur ]1;+[,
23
1x x x x
x   
.
 Si x=1, les courbes C1, C2, C3, C4 et C5 se coupent. Donc si x=1 ,
32 11x x x x x
.
 Si x=0, les courbes C2, C3, C4 et C5 se coupent. Donc si x=0 ,
32 0x x x x   
.
Conclusion : pour comparer, ou ordonner un nombre, son carré et sa
racine carré, il faut comparer ce nombre à 0 et 1.
Astuce : on peut voir une racine carré comme une puissance ½ (
1/2
xx
) et l'inverse comme une puissance 1(
1
1x
x
) et
1
xx
.
Alors si x]0;1[, plus la puissance est grande, plus le nombre est petit, et
si x]1;+[, plus la puissance est grande, plus le nombre est grand.
Exemple : Soit le réel
21
23
. On remarque que
21
01
23
, donc
32
2 1 2 1 2 1 2 1 2 3
2 3 2 3 2 3 2 3 2 1
Technique 11 – D'une courbe à l'autre, Fonctions associées :
La fonction u est une fonction (en général, une fonction de référence).
 Addition par un nombre : Sur un intervalle I, pour tout réel k, les
fonctions u et f=u+k ont les mêmes variations.
 Multiplication par un nombre positif : Sur un intervalle I, pour
tout réel >0, les fonctions u et f=u ont les mêmes variations.
 Multiplication par un nombre négatif : Sur un intervalle I, pour
tout réel <0, les fonctions u et f=u ont des variations contraires.
 Racine d'une fonction : Sur un intervalle I, où la fonction u est
positive ou nulle, les fonctions u et f=
u
ont les mêmes
variations (car la fonction racine carrée est strictement croissante
donc conserve l'ordre et aussi les variations).
 Inverse d'une fonction strictement positive : Sur un intervalle I,
où la fonction u est strictement positive , les fonctions u et
1
fu
ont des variations contraires (car la fonction inverse est strictement
décroissante sur ]0;+∞[, donc change l'ordre et change aussi les
variations).
 Inverse d'une fonction strictement négative : Sur un intervalle I,
où la fonction u est strictement négative, les fonctions u et
1
fu
ont des variations contraires (car la fonction inverse est strictement
décroissante sur ]∞;0[, donc change l'ordre et change aussi les
variations).
 Carré d'une fonction positive : Sur un intervalle I, où la fonction
u est strictement positive, la fonction u et u² ont les mêmes
variations (car sur [0;+∞[, la fonction carré est strictement
croissante donc conserve l'ordre et aussi les variations).
 Carré d'une fonction négative : Sur un intervalle I, où la fonction
u est strictement négative, la fonction u et u² ont des variations
contraires (car sur ]∞;0], la fonction carré est strictement
décroissante donc change l'ordre et change aussi les variations).
Nombres de conditions requises :
 Addition par un nombre : Une seule condition : connaître les
variations de u.
 Multiplication par un nombre : Deux conditions : le signe du
coefficient multiplicateur ET les variations de u.
 Racine d'une fonction : Deux conditions : la positivité ET les
variations de la fonction u.
 Inverse d'une fonction : Deux conditions : le signe de la fonction
ET les variations de la fonction u.
Exemples :
 Addition par un nombre : Soit
( ) ²u x x
et
( ) ( ) 7 ² 7f x u x x   
. La fonction u est strictement croissante
sur [0;+[. Par addition d'un nombre (7), la fonction f est aussi
strictement croissante sur [0;+[.
 Inverse d'une fonction : Soit
( ) 2 1u x x
et
11
() ( ) 2 1 fx u x x
.
(i) La fonction u est strictement croissante et strictement positive
sur ]1/2;+[. Par inverse d'une fonction, la fonction f est
strictement décroissante (et strictement positive) sur ]1/2;+[.
(ii) La fonction u est strictement croissante et strictement négative
sur ];1/2[. Par inverse d'une fonction, la fonction f est
strictement croissante (et strictement négative) sur ];1/2[.
 Multiplication ppar un nombre négatif : Soit
3
()u x x
et
3
( ) 3 ( ) 3f x u x x   
. La fonction u est strictement croissante sur
4. Par produit d'un nombre négatif (3), la fonction f est
strictement décroissante sur 4.
 Racine d'une fonction : Soit
( ) 2u x x
et
( ) ( ) 2f x u x x  
. La fonction u est strictement croissante et
positive ou nulle sur [2;+[. Par racine carré d'une fonction, la
fonction f est strictement croissante sur [2;+[.
Exemple n°1 de tableau de variations :
Soit f la fonction définie sur 4\{2} par :
1
( ) 2 ( 3) 2 fx x
.
Posons alors la fonction de référence
( ) 2u x x
.
L'algorithme de passage de u à f est alors : inverse ; (3) ; +2.
D'où le tableau de variations suivant :
Exemple n°2 de tableau de variations :
Soit f la fonction définie sur ]∞;2]∪[2;+∞[ par
( ) 3 2 ² 4f x x   
.
Posons alors la fonction de référence
( ) ²u x x
.
L'algorithme de passage de u à f est alors : 4 ; racine carré ; 2 ; +3
D'où le tableau de variations suivant :