Sujet d`ordre général

hn
Guy COLLIN, 2014-12-29
MÉTHODES THÉORIQUES
D’ÉTUDE DU NUAGE
ÉLECTRONIQUE
Chapitre 5

hn
2014-12-29
L’électron autour du noyau
Pour compléter l’étude de l’électron, il est tout
naturel de connaître les propriétés de l’assemblage
des électrons dans un atome, autour d’un noyau.
Comment peut-on étudier cet assemblage ?
Quelles sont les lois qui régissent cet assemblage ?
Comment la mécanique classique peut aider à la
compréhension de ce système « solaire » ?
Qu’est-ce que la mécanique ondulatoire vient apporter
à la connaissance de cet assemblage ?

hn
2014-12-29
Introduction
RUTHERFORD a montré qu’un atome possède un
noyau central très petit et des électrons tournant sur
des orbites.
BOHR a proposé une explication détaillée des
spectres atomiques et, en particulier, du spectre de
l’hydrogène.
Mais nous verrons que la mécanique classique est
impuissante à décrire les phénomènes.
Seule l’assimilation de l’électron à une onde conduit
à une théorie cohérente.

hn
2014-12-29
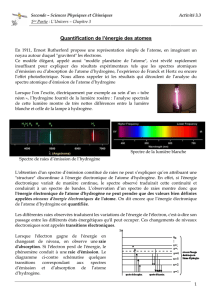
Le spectre de l’hydrogène
Si on provoque une décharge électrique dans une
atmosphère raréfiée d’hydrogène, on observe
l’émission d’une lumière pourpre.
Cette lumière analysée au spectrographe peut être
séparée en un certain nombre de fréquences.
Ce spectre de raies est caractéristique de l’élément.
Ces mêmes raies ou fréquences apparaissent
également en absorption (raies noires sur fond
continu) dans le spectre du soleil par exemple.

hn
2014-12-29
Le spectre de l’hydrogène :
dispositif expérimental
Faisceau de lumière
provenant d’une
lampe à hydrogène Écran
Fentes Système dispersif