TSMP :

1
TS Cours Physique
Chap 10 : La SPECTROSCOPIE et le modèle corpusculaire de la lumière
Relire le chap 16 de 1SMP puis chercher les exercices suivants :
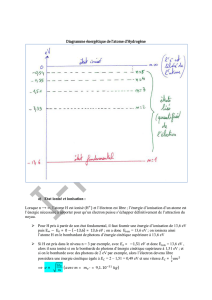
Ex1 : L’effet photoélectrique : le travail d'extraction d'un électron du zinc est W0 = 3,30 eV.
1. Calculer la fréquence seuil et la longueur d'onde seuil du zinc.
2. On éclaire le zinc par une radiation UV de longueur d'onde = 0,250 µm. Calculer l'énergie cinétique maximale de sortie des
électrons et leur vitesse. On donne me- = 9,1.10-31 kg.
3. On éclaire le zinc par la lumière d'un arc électrique en interposant une plaque de verre qui absorbe les ondes de longueur d'onde
inférieure à 0,420 µm. Un effet photoélectrique est-il observé ?
Ex2 et Ex3 : Exercices 32 et 37 sur feuilles (en entier avec les interférences) Ex4 : Exercice 35 annales (écrit 2004)
Ex5 : proposition bac 2004 NIVEAUX D’ENERGIE
1. Atome d’hydrogène
Les niveaux d’énergie de l’atome d’hydrogène sont caractérisés par la relation : En = - E0 / n2
a. Que représentent E0 et n ?
b. Expliquer brièvement l’existence de raies dans le spectre d’émission de l’atome d’hydrogène.
c. Montrer que les longueurs d’onde mp des radiations émises par l’atome d’hydrogène obéissent à la loi :
1/mp = R1(1/p2 – 1/m2) où m et p sont des entiers naturel tels que m > p et R1 est une constante dont on donnera
l’expression en fonction de E0, de la constante de Planck h et de la vitesse de la lumière dans le vide c.
d. Nommer cette constante, trouver sa dimension et calculer sa valeur en donnant trois chiffres significatifs.
2. Ion hélium He+
Le spectre de l’ion hélium He+ comporte, entre autres, des raies de longueurs d’onde 23,74 nm ; 24,30 nm ; 25,63 nm et 30,38 nm.
Ces raies correspondent aux transitions énergétiques caractérisées par p = 1 et m = 2, 3, 4 et 5.
a. Trouver le couple (p, m) correspondant à chaque raie.
b. Vérifier que les valeurs de longueurs d’onde sont numériquement compatibles avec une relation de la forme :
1/mp = R2(1/p2 – 1/m2) où R2 est une constante identique pour les quatre raies.
b. Pour les quatre raies, vérifier que la valeur de R2 est constante à trois chiffres significatifs près
c. Comparer R2 à R1.
3. Ion lithium Li2+
Le spectre de l’ion lithium Li2+comporte, des raies dont les longueurs d’onde obéissent à une loi du type précédent :
1/mp = R3(1/p2 – 1/m2) où R3 est une constante de valeur 9,86.107 m-1.
a. Comparer R3 à R1 et en déduire une relation simple entre la constante R et le numéro atomique Z de l’élément
correspondant dans les trois cas étudiés.
b. Trouver le point commun entre l’atome H et les ions He+ et Li2+ qui explique la ressemblance des spectres de ces trois
éléments.
On donne : E0 = 13,6 eV, constante de Planck h = 6,62.10-34 J.s vitesse de la lumière dans le vide c = 3,00.108 m.s-1
numéros atomiques : Z = 1 pour H, Z = 2 pour He et Z = 3 pour Li
Ex6 : On donne le diagramme des niveaux d’énergie du sodium.
1. Que signifie le terme « quantifié », lorsqu’on dit que les niveaux d’énergie de l’atome de
sodium sont quantifiés ?
2. Déterminer la longueur d’onde du photon émis lorsque l’atome de sodium se désexcite de
son état E3 vers son état fondamental. A quel domaine des ondes électromagnétiques ce
rayonnement appartient-il ?
3. Lorsqu’il est en état E3, le sodium peut-il émettre un photon de fréquence 2,66.1014 Hz ?
4. Quelle est l’énergie d’ionisation de l’atome de sodium ?
5. Quel type se spectre obtient-on avec une lampe à vapeurs de sodium (non ionisé) ? A quoi
ressemble-t-il ?